题目内容
已知θ=kπ±α(k∈Z),探究θ与α的三角函数之间的关系.
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:本题利用平面直角坐标系通过分类讨论研究两角的终边位置,得到它们之间 的关系,得到本题结论.
解答:
解:∵θ=kπ±α(k∈Z),
∴θ=kπ+α或θ=kπ-α(k∈Z),
(1)当θ=kπ+α(k∈Z)时,
①当k为偶数时,k=2m,m∈Z,
θ=kπ+α=2mπ+α,θ与α的终边相同,
②当k为奇数时,k=2m+1,m∈Z,
θ=kπ+α=2mπ+π+α,θ与α的终边关于原点对称.
(2)当θ=kπ-α(k∈Z)时,
①当k为偶数时,k=2m,m∈Z,
θ=kπ+α=2mπ-α,θ与α的终边关于x轴对称,
②当k为奇数时,k=2m+1,m∈Z,
θ=kπ+α=2mπ+π-α,θ与α的终边关于y轴对称.
综上,角θ与α的终边可能相同、可能关于y轴对称、可能关于x轴对称、可能关于原点对称.
∴θ=kπ+α或θ=kπ-α(k∈Z),
(1)当θ=kπ+α(k∈Z)时,
①当k为偶数时,k=2m,m∈Z,
θ=kπ+α=2mπ+α,θ与α的终边相同,
②当k为奇数时,k=2m+1,m∈Z,
θ=kπ+α=2mπ+π+α,θ与α的终边关于原点对称.
(2)当θ=kπ-α(k∈Z)时,
①当k为偶数时,k=2m,m∈Z,
θ=kπ+α=2mπ-α,θ与α的终边关于x轴对称,
②当k为奇数时,k=2m+1,m∈Z,
θ=kπ+α=2mπ+π-α,θ与α的终边关于y轴对称.
综上,角θ与α的终边可能相同、可能关于y轴对称、可能关于x轴对称、可能关于原点对称.
点评:本题考查了角的终边位置关系和分类讨论的数学思想,本题难度不大,属于基础题.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
下列命题中,真命题是( )
| A、“a≤b”是“a+c≤b+c”的充分不必要条件 | ||||||||
| B、“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题 | ||||||||
| C、二进制数1010(2) 可表示为三进制数110(3) | ||||||||
D、“平面向量
|
若命题“p∨q”与命题“¬p”都是真命题,则( )
| A、命p不一定是假命题 |
| B、命题q一定是真命题 |
| C、命题q不一定是真命题 |
| D、命题p与命题q同真同假 |
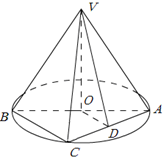 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.