题目内容
求函数y=7-6sinx-2cos2x的最值．
考点：三角函数的最值
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系，可得y═7-6sinx-2（1-sin2x），再根据正弦函数的值域，二次函数的性质求得y的值域．
解答：
解：令t=sinx∈[-1，1]，则函数y=7-6sinx-2cos2x=7-6sinx-2（1-sin2x）=2t2-6t+9=2(t-
)2+
，
故当t=1时，y取得最小值为5，当t=-1时，函数取得最大值为 17，
故函数的值域为[5，17]．
| 3 |
| 2 |
| 9 |
| 2 |
故当t=1时，y取得最小值为5，当t=-1时，函数取得最大值为 17，
故函数的值域为[5，17]．
点评：本题主要考查同角三角函数的基本关系，正弦函数的值域，二次函数的性质，属于基础题．
练习册系列答案
相关题目
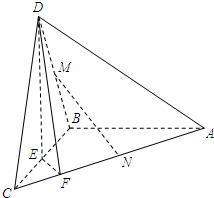如图，在三棱锥D-ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC，E为BC的中点，F在棱AC上，且AF=3FC，