Question

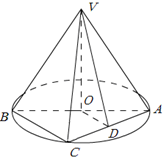如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，D是AC的中点，已知AB=2，VA=VB=VC=2．
（1）求证：AC⊥平面VOD；
（2）VD与平面ABC所成角的正弦值；
（3）求三棱锥C-ABV的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面所成的角

专题：空间位置关系与距离

分析：（1）得出AC⊥VO，AC⊥VD即可证明．（2）根据棱锥V-ABC的体积为V_V-ABC=

1

3

S_△ABC•VO=

1

3

×1×

3

可求得．

解答： 解：（1）∵VA=VB，O为AB中点，
∴VO⊥AB，连接OC，在△VOA和△VOC中，OA=OC，VO=VO，VA=VC，
∴△VOA≌△VOC，∠VOA=∠VOC=90°，
∴VO⊥0C
∵AB∩OC=0，AB?平面ABC，OC?平面ABC，
∴VO⊥平面ABC，
∵AC?平面ABC，
∴AC⊥VO，
又∵VA=VC，D是AC的中点，∴AC⊥VD，
∵VO?平面VOD，VD?平面VOD，VD∩VO=V，
∴AC⊥平面VOD，
（2）由（1）知VO是棱锥V-ABC的高，且VO=

VA2-AO2

=

3

．
又∵点C是弧的中点，∴CO⊥AB，且CO=1，AB=2，
∴三角形ABC的面积S_△ABC=

1

2

AB•CD=

1

2

×2×1=1，
∴棱锥V-ABC的体积为V_V-ABC=

1

3

S_△ABC•VO=

1

3

×1×

3

故棱锥C-ABV的体积为

3

3

，

点评：本题考查了直线与平面的垂直问题，体积计算问题，属于中档题，思路要清晰，认真．