题目内容
下列命题中,真命题是( )
| A、“a≤b”是“a+c≤b+c”的充分不必要条件 | ||||||||
| B、“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题 | ||||||||
| C、二进制数1010(2) 可表示为三进制数110(3) | ||||||||
D、“平面向量
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:由充要条件的概念结合不等式的性质判断A;写出命题的逆否命题判断B,化二进制为三进制判断C,举特例判断D.
解答:
解:由a≤b能得到a+c≤b+c,由a+c≤b+c能得到a≤b,
∴“a≤b”是“a+c≤b+c”的充分必要条件,选项A错误;
已知x,y∈R,若x+y≠6,则x≠2或y≠4的逆否命题为:
已知x,y∈R,若x=2且y=4,则x+y=6,是真命题,
∴“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题,选项B正确;
由1010(2)=0×1+1×2+0×4+1×8=10(10),可得二进制数1010(2) 可表示为三进制数101(3),选项C错误;
平面向量
与
的夹角是钝角,则
•
<0,
由
•
<0,向量
与
的夹角可能是180°,选项D错误.
故选:B.
∴“a≤b”是“a+c≤b+c”的充分必要条件,选项A错误;
已知x,y∈R,若x+y≠6,则x≠2或y≠4的逆否命题为:
已知x,y∈R,若x=2且y=4,则x+y=6,是真命题,
∴“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题,选项B正确;
由1010(2)=0×1+1×2+0×4+1×8=10(10),可得二进制数1010(2) 可表示为三进制数101(3),选项C错误;
平面向量
| a |
| b |
| a |
| b |
由
| a |
| b |
| a |
| b |
故选:B.
点评:本题考查了命题的真假判断与应用,考查了充分条件、必要条件的判断方法,训练了进位制的转化,是中档题.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若圆(x-a)2+(y-b)2=c2和圆(x-b)2+(y-a)2=c2相切,则( )
| A、(a-b)2=c2 |
| B、(a-b)2=2c2 |
| C、(a+b)2=c2 |
| D、(a+b)2=2c2 |
已知△ABC中c=4,a=4
,C=30°,则A等于( )
| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
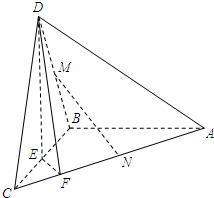 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,