题目内容
如图,已知△ABC中,AB=
,CD=5,∠ABC=
,∠ACB=
,求AD的长度.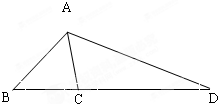
3
| ||
| 2 |
| π |
| 4 |
| π |
| 3 |

考点:三角形中的几何计算
专题:计算题,解三角形
分析:由正弦定理先求得AC的值,从而由余弦定理得:AD2=AC2+CD2-2AC•CDcos∠ACD=32+52-2×3×5×(-
)=49,即可求出AD的值.
| 1 |
| 2 |
解答:
解:由正弦定理得:
=
,所以AC=3;
由余弦定理得:AD2=AC2+CD2-2AC•CDcos∠ACD=32+52-2×3×5×(-
)=49,
所以AD=7.
| AC |
| sin45° |
| ||||
| sin60° |
由余弦定理得:AD2=AC2+CD2-2AC•CDcos∠ACD=32+52-2×3×5×(-
| 1 |
| 2 |
所以AD=7.
点评:本题主要考察了正弦定理、余弦定理的综合应用,属于基础题.

练习册系列答案
相关题目
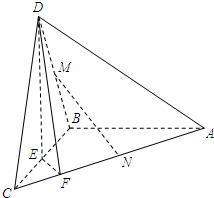 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,