题目内容
已知函数f(x)=
,求f(x)的最大值,最小值.
|
考点:分段函数的应用
专题:函数的性质及应用
分析:先研究函数在每一段的单调性,分别求出它们的最值,最后大中取大,小中取小.
解答:
解:对于函数f(x)=
,
①当-1≤x≤1时,f(x)=x2在[-1,0]上递减,在[0,1]上递增;
所以此时ymin=f(0)=0,ymax=f(1)=f(-1)=1;
②当x>1时,f(x)=
是递减函数,所以y<f(1)=1,
即此时0<y<1;
综合①②可知原函数的最大值为f(1)=1,最小值为f(0)=0.
|
①当-1≤x≤1时,f(x)=x2在[-1,0]上递减,在[0,1]上递增;
所以此时ymin=f(0)=0,ymax=f(1)=f(-1)=1;
②当x>1时,f(x)=
| 1 |
| x |
即此时0<y<1;
综合①②可知原函数的最大值为f(1)=1,最小值为f(0)=0.
点评:本题考查分段函数的性质,一般来讲分段函数的处理原则:分段函数,分段处理.如本题求最值,应先在每一段上求它们的最大(小)值,最后大中取大.小中取小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
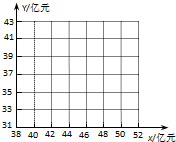 某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如下表所示:
某市居民1999~2003年货币收入x与购买商品支出Y的统计资料如下表所示:
