题目内容

若f（x）=
2-x，x∈(-∞，1]
log81x，x∈(1，+∞)
，求满足f（x）=
1
4
的x的值．
考点：函数的零点,函数的值,对数的运算性质
专题：计算题,函数的性质及应用
分析：由分段函数式，得到
x≤1
2-x=
1
4
或
x＞1
log81x=
1
4
，由指数和对数的运算法则，即可得到答案．
解答： 解：
x≤1
2-x=
1
4
或
x＞1
log81x=
1
4
，
则
x≤1
x=2
 或
x＞1
x=81
1
4
=3
，
所以x=3．
点评：本题考查分段函数及运用，考查分段函数值，应注意各段自变量的范围，考查指数和对数的运算，属于基础题．
练习册系列答案
相关题目
（1）求y=
x2+5
x2+4
的最小值；
（2）若a＞0，b＞0，且a2+
b2
2
=1，求a
1+b2
的最大值．
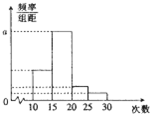对某校高一年级学生参加社区服务次数统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组频数频率
[10，15）50.25
[15，20）12n
[20，25）mp
[25，30）10.05
合计M1
（Ⅰ）求出表中M，p及图中a的值；
（Ⅱ）若该校高一学生有360人，试估计他们参加社区服务的次数在区间[15，20）内的人数；
（Ⅲ）学校决定对参加社区服务的学生进行表彰，对参加活动次数的区间[25，30）内的学生发放价值80元的学习用品，对参加活动次数在区间[20，25）内的学生发放价值60元的学习用品，对参加活动次数在区间[15，20）内的学生发放价值40元的学习用品，对参加活动次数在区间[10，15）内的学生发放价值20元的学习用品，在所取样本中，任意取了2人，并设X为此2人所获得用品价值之差的绝对值，求X的分布列与数学期望E（X）．
已知m＞0，n＞0，且
1
m
+
9
n
=1，证明：m+n≥16．
已知函数f（x）=ax2+bx+c（a≠0），判断并证明函数f（x）的单调性．
已知函数f（x）=
x2(-1≤x≤1)
1
x
(x＞1)
，求f（x）的最大值，最小值．
（1）已知双曲线的中心在原点，焦点F1，F2在坐标轴上，离心率为
2
，且过点（4，-
10
）．求双曲线的标准方程；
（2）已知曲线C上任意一点M到点F（0，1）的距离比它到直线l：y=-2的距离小1．求曲线C的方程．
若函数f（x）=ax3-bx+4，当x=2时，函数f（x）有极值，且函数f（x）图象上以点A（3，f（3））为切点的切线与直线5x-y+1=0平行．
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调区间；
（3）若方程f（x）=k有3个解，求实数k的取值范围．
已知函数f（x）=ex，g（x）=ax2+bx+1，当a=0时，若f（x）≥g（x）对任意x恒成立，求b的取值集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网