题目内容
已知函数y=cos2x+sinx+2.
(1)若x∈R,求该函数的最大值;
(2)若x∈[0,2π),且y>3,求x的取值范围.
(1)若x∈R,求该函数的最大值;
(2)若x∈[0,2π),且y>3,求x的取值范围.
考点:三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)利用二倍角的余弦降幂,转化为关于sinx的关系式,配方即可求得该函数的最大值;
(2)由y>3,可得2sin2x-sinx<0,继而可得0<sinx<
,又x∈[0,2π),从而可得x的取值范围.
(2)由y>3,可得2sin2x-sinx<0,继而可得0<sinx<
| 1 |
| 2 |
解答:
解:(1)y=cos2x+sinx+2=1-2sin2x+sinx+2=-2sin2x+sinx+3=-2(sinx-
)2+
,
当sinx=
时,该函数的最大值为
;
(2)y>3,即-2sin2x+sinx+3>3,2sin2x-sinx<0,解得0<sinx<
,又x∈[0,2π),
所以x的取值范围是(0,
)∪(
,2π).
| 1 |
| 4 |
| 25 |
| 8 |
当sinx=
| 1 |
| 4 |
| 25 |
| 8 |
(2)y>3,即-2sin2x+sinx+3>3,2sin2x-sinx<0,解得0<sinx<
| 1 |
| 2 |
所以x的取值范围是(0,
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查三角函数中的恒等变换应用,考查正弦函数的单调性与最值,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
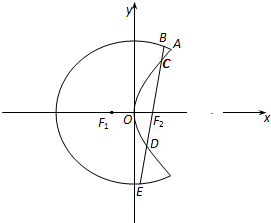 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”.若|AF1|=7,|AF2|=5.
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”.若|AF1|=7,|AF2|=5.