题目内容
已知α是三角形的一个内角，且满足sinα+cosα=
，求tanα．
| 1 |
| 5 |
考点：同角三角函数间的基本关系
专题：三角函数的求值
分析：将已知等式两边平方，利用完全平方公式化简，整理后判断出sinα与cosα的正负，利用同角三角函数间基本关系得到sin2α+cos2α=1，联立求出sinα与cosα的值，即可确定出tanα的值．
解答：
解：将sinα+cosα=
，两边平方得：（sinα+cosα）2=1+2sinαcosα=
，
∴sinαcosα=-
＜0，即sinα＞0，cosα＜0，
与sin2α+cos2α=1，联立得：
，
∴
，
则tanα=-
．
| 1 |
| 5 |
| 1 |
| 25 |
∴sinαcosα=-
| 12 |
| 25 |
与sin2α+cos2α=1，联立得：
|
∴
|
则tanα=-
| 4 |
| 3 |
点评：此题考查了同角三角函数间的基本关系，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
如果数列{an}满足an+1=
且a1=2，则数列{an}的通项公式是（ ）
| an |
| an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
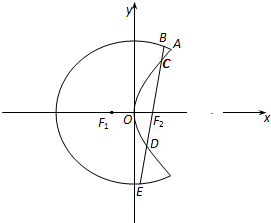如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．