题目内容
如图，小圆圈表示网络的结点，结点之间的箭头表示它们有网线相联，连线标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A向结点G传递信息，信息可以分开沿不同的路线同时传递．则单位时间内传递的最大信息量为（ ）
| A、31 | B、6 | C、10 | D、14 |
考点：进行简单的合情推理
专题：计算题,推理和证明
分析：据题意，计算各个路线的最大信息量，相加可得答案．
解答：
解：依题意，首先找出A到G的路线，一共有三条，
三条线路最大信息量分别为2，2，2
故从A到G的最大信息量为2+2+2=6，
故选：B．
三条线路最大信息量分别为2，2，2
故从A到G的最大信息量为2+2+2=6，
故选：B．
点评：本题考查了分类计数的加法原理，完成时注意每条线跑中每节点中最小的数字即这个条线路中单位时间内可以通过的最大信息量．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
直线y-kx-1=0（k∈R）与椭圆
+
=1恒有公共点，则m的取值范围是 （ ）
| x2 |
| 5 |
| y2 |
| m |
| A、m＞5 | B、0＜m＜5 |
| C、m＞1 | D、m≥1且m≠5 |
已知sinα+cosα=
，则sinαcosα=（ ）
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
将棱长为a 的正方体ABCD-A1B1C1D1沿截面DA1C1截去一个角后，剩下的几何体体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如果数列{an}满足an+1=
且a1=2，则数列{an}的通项公式是（ ）
| an |
| an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过已知点A（2，3），B（1，5）的直线AB的斜率是（ ）
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
已知直线的点斜式方程是y+1=x-2，那么此直线的斜率为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
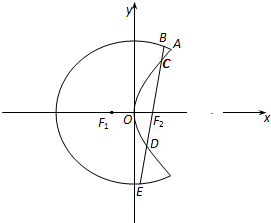如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．