题目内容
已知集合A={x|-2≤x≤4}，B={x|x＞a}．
（Ⅰ）A∩B=∅，求实数a的取值范围；
（Ⅱ）A∩B≠∅且A∩B≠A，求实数a的取值范围．
（Ⅰ）A∩B=∅，求实数a的取值范围；
（Ⅱ）A∩B≠∅且A∩B≠A，求实数a的取值范围．
考点：交集及其运算
专题：集合
分析：（Ⅰ）利用不等式性质和交集定义能求出实数a的取值范围．
（Ⅱ）当A∩B=A时，a＜-2，由此能求出当A∩B≠φ且A∩B≠A时，实数a的取值范围．
（Ⅱ）当A∩B=A时，a＜-2，由此能求出当A∩B≠φ且A∩B≠A时，实数a的取值范围．
解答：
解：（Ⅰ）∵A={x|-2≤x≤4}，B={x|x＞a}，A∩B=φ，
∴a＞4，即实数a的取值范围是（4，+∞）．
（Ⅱ）∵当A∩B=A时，a＜-2，
∴当A∩B≠φ且A∩B≠A时，
-2≤a≤4，即实数a的取值范围是[-2，4]．
∴a＞4，即实数a的取值范围是（4，+∞）．
（Ⅱ）∵当A∩B=A时，a＜-2，
∴当A∩B≠φ且A∩B≠A时，
-2≤a≤4，即实数a的取值范围是[-2，4]．
点评：本题考查实数的取值范围的求法，是基础题，解题时要注意交集性质的合理运用．
练习册系列答案
相关题目
已知sinα+cosα=
，则sinαcosα=（ ）
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
已知直线的点斜式方程是y+1=x-2，那么此直线的斜率为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、1 |
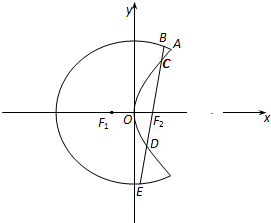如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．