题目内容
20．
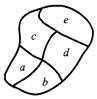某社区新建了一个休闲小公园，几条小径将公园分成5块区域，如图，社区准备从4种颜色不同的花卉中选择若干种种植在各块区域，要求每个区域随机用一种颜色的花卉，且相邻区域（用公共边的）所选花卉颜色不能相同，则不同种植方法的种数共有（ ）| A． | 96 | B． | 114 | C． | 168 | D． | 240 |
分析 根据题意，依次分析e、c、d以及a、b区域的选择情况数目，进而由分步计数原理计算可得答案．
解答 解：根据题意，分4步进行分析：
对于e区域，有4种花卉可选，即有4种情况，
对于c区域，与e区域相邻，有3种情况，
对于d区域，与e、c区域相邻，有2种情况，
对于a、b区域，分2种情况讨论：
若其与d区域种植的相同，则b区域有3种花卉可选，即有3种情况，此时a、b区域有1×3=3种情况，
若a区域与d区域种植的步相同，则a区域有2种情况，b区域有2种情况，此时a、b区域有2×2=4种情况，
则a、b区域共有3+4=7种情况，
则不同种植方法的种数共有4×3×2×7=168种；
故选：C．
点评 本题考查排列组合的应用，涉及分步计数原理的应用，注意分析图形中区域相邻的情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．
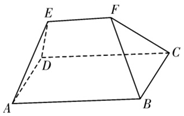中国古代数学家名著《九章算术》中记载：“刍甍者，下有袤有广，而上有袤无广．刍，草也．甍，屋盖也．”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱．刍甍字面意思为茅草屋顶．”现有一个刍甍如图所示，四边形ABCD为正方形，四边形ABFE、CDEF为两个全等的等腰梯形，AB=4，EF$\underset{∥}{=}$$\frac{1}{2}$AB，若这个刍甍的体积为$\frac{40}{3}$，则异面直线AB与CF所成角的余弦值为（ ）
中国古代数学家名著《九章算术》中记载：“刍甍者，下有袤有广，而上有袤无广．刍，草也．甍，屋盖也．”翻译为“底面有长有宽为矩形，顶部只有长没有宽为一条棱．刍甍字面意思为茅草屋顶．”现有一个刍甍如图所示，四边形ABCD为正方形，四边形ABFE、CDEF为两个全等的等腰梯形，AB=4，EF$\underset{∥}{=}$$\frac{1}{2}$AB，若这个刍甍的体积为$\frac{40}{3}$，则异面直线AB与CF所成角的余弦值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{5}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
12．在△ABC中，D，E分别为BC，AB的中点，F为AD的中点，若$\overrightarrow{AB}•\overrightarrow{AC}=-1$，AB=2AC=2，则$\overrightarrow{CE}•\overrightarrow{AF}$的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{4}$ |