题目内容
9.若变量x,y满足$\left\{\begin{array}{l}{2x-y-6≤0}\\{x-y+3≥0}\\{x≥1}\end{array}\right.$,目标函数z=2ax+by(a>0,b>0)取得最大值的是6,则$\frac{1}{a}+\frac{2}{b}$的最小值为7+4$\sqrt{3}$.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,确定z取最大值点的最优解,利用基本不等式的性质,利用数形结合即可得到结论.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=2ax+by(a>0,b>0)得y=-$\frac{2a}{b}$x+$\frac{k}{b}$,
则直线的斜率k=-$\frac{2a}{b}$<0,截距最大时,z也最大.
平移直y=-$\frac{2a}{b}$+$\frac{k}{b}$,由图象可知当直线y=-$\frac{2a}{b}$+$\frac{k}{b}$经过点A时,
直线y=-$\frac{2a}{b}$+$\frac{k}{b}$截距最大,此时z最大,
由$\left\{\begin{array}{l}{2x-y-6=0}\\{x-y+3=0}\end{array}\right.$,解得x=9,y=12
即A(9,12),
此时z=18a+12b=6,
即3a+2b=1,
∴$\frac{1}{a}+\frac{2}{b}$=($\frac{1}{a}+\frac{2}{b}$)(3a+2b)=3+4+$\frac{2b}{a}$+$\frac{6a}{b}$
≥7+2$\sqrt{\frac{2b}{a}•\frac{6a}{b}}$=7+4$\sqrt{3}$,当且仅当b=$\sqrt{3}$a时,取等号,
故$\frac{1}{a}+\frac{2}{b}$的最小值为7+4$\sqrt{3}$,
故答案为:7+4$\sqrt{3}$.
点评 本题主要考查线性规划的应用,利用z的几何意义先求出最优解是解决本题的关键,利用基本不等式的解法和结合数形结合是解决本题的突破点.

练习册系列答案
相关题目
20.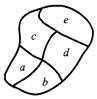 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
 某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )
某社区新建了一个休闲小公园,几条小径将公园分成5块区域,如图,社区准备从4种颜色不同的花卉中选择若干种种植在各块区域,要求每个区域随机用一种颜色的花卉,且相邻区域(用公共边的)所选花卉颜色不能相同,则不同种植方法的种数共有( )| A. | 96 | B. | 114 | C. | 168 | D. | 240 |
18.某商家在网上销售一种商品,从该商家的销售数据中抽取6天的价格与销量的对应数据,如下表所示:
(Ⅰ)由表中数据,看出可用线性回归模型拟合y与x的关系,试求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,并预测当价格为1000元时,每天的商品的销量为多少;
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率作为客户A,B购买此商品的概率,而客户C,D购买此商品的概率均为$\frac{1}{2}$,设这4位客户中购买此商品的人数为X,求X的分布列和数学期望.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 价格x(百元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 销量y(件/天) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)若以从这6天中随机抽取2天,至少有1天的价格高于700元的概率作为客户A,B购买此商品的概率,而客户C,D购买此商品的概率均为$\frac{1}{2}$,设这4位客户中购买此商品的人数为X,求X的分布列和数学期望.
参考数据:$\sum_{i=1}^{6}$xiyi=3050,$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=271.
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$.
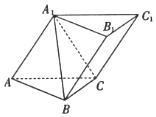 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.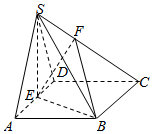 已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.
已知四棱锥S-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,SA=SD=$\sqrt{5},SB=\sqrt{7}$,点E是棱AD的中点,点F在棱SC上,且$\frac{SF}{SC}$=λ,SA∥平面BEF.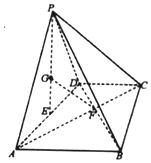 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F