题目内容
已知数列{an}中,a1=2,an+1=an2+2an(n∈N+).
(1)证明:数列{log2(an+1)}是等比数列,并求数列{an}的通项公式;
(2)记bn=
+
,求数列{bn}的前n项和Sn.
(1)证明:数列{log2(an+1)}是等比数列,并求数列{an}的通项公式;
(2)记bn=
| 1 |
| an |
| 1 |
| an+2 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知得log2(an+1+1)=log2(an+1)2=2log2(an+1),log2(a1+1)=log23,由此能证明数列{log2(an+1)}是首项为log23,公比为2的等比数列,从而求出an=32n-1-1.
(2)由an+1=an2+2an(n∈N+),两边取对数,得
=
-
,从而
=
-
,进而bn=2(
-
),由此利用裂项求和法能求出数列{bn}的前n项和Sn.
(2)由an+1=an2+2an(n∈N+),两边取对数,得
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+2 |
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
解答:
(1)证明:∵数列{an}中,a1=2,an+1=an2+2an(n∈N+),
∴an+1+1=an2+2an+1=(an+1)2,
∴log2(an+1+1)=log2(an+1)2=2log2(an+1),
∴
=2,
又log2(a1+1)=log23,
∴数列{log2(an+1)}是首项为log23,公比为2的等比数列,
∴log2(an+1)=log23•2n-1,
∴an+1=32n-1,
∴an=32n-1-1.
(2)解:∵an+1=an2+2an(n∈N+),
两边取对数,得
=
-
,
即
=
-
,
∵bn=
+
,∴bn=2(
-
),
∴Sn=2[(
-
)+(
-
)+…+(
-
)]
=2(
-
)
=1-
.
∴an+1+1=an2+2an+1=(an+1)2,
∴log2(an+1+1)=log2(an+1)2=2log2(an+1),
∴
| log2(an+1+1) |
| log2(an+1) |
又log2(a1+1)=log23,
∴数列{log2(an+1)}是首项为log23,公比为2的等比数列,
∴log2(an+1)=log23•2n-1,
∴an+1=32n-1,
∴an=32n-1-1.
(2)解:∵an+1=an2+2an(n∈N+),
两边取对数,得
| 2 |
| an+1 |
| 1 |
| an |
| 1 |
| an+2 |
即
| 1 |
| an+2 |
| 1 |
| an |
| 2 |
| an+1 |
∵bn=
| 1 |
| an |
| 1 |
| an+2 |
| 1 |
| an |
| 1 |
| an+1 |
∴Sn=2[(
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
=2(
| 1 |
| a1 |
| 1 |
| an+1 |
=1-
| 2 |
| 32n-1 |
点评:本题考查等比数列的证明,考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
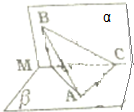 在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
在直二面角α-MN-β中,等腰直角△ABC的斜边BC?α,一直角边AC?β,BC与β所成角的正弦值为
| ||
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
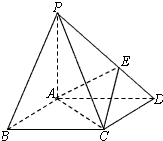 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=3,PB=PD=3
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC=3,PB=PD=3