题目内容
7个人站在一排.
(1)甲、乙2人必须站在两端,有多少种排法?
(2)甲、乙、丙3人必须排在一起,有多少种排法?
(3)甲不在排头且乙不在排尾,有多少种排法?
(1)甲、乙2人必须站在两端,有多少种排法?
(2)甲、乙、丙3人必须排在一起,有多少种排法?
(3)甲不在排头且乙不在排尾,有多少种排法?
考点:计数原理的应用
专题:排列组合
分析:本题(1)可先将甲、乙2人站在两端,其余5人全排列,可得本题结论;(2)本题可先将甲、乙、丙3人捆绑在一起,再进行排列,得到本题结论;(3)可以先全排列,再排除甲在排头和乙在排尾的情况,得到本题结论.
解答:
解:(1)∵甲、乙2人必须站在两端,
∴先将甲、乙2人站在两端,其余5人全排列,
得到:
•
=2×5×4×3×2×1=240(种)
(2)甲、乙、丙3人必须排在一起,
可先将甲、乙、丙3人捆绑在一起,再进行排列,
得到:
•
=6×120=720(种)
(3)甲不在排头且乙不在排尾,
先全排列,再排除甲在排头和乙在排尾的情况,
得到:
-
-
+
=3720(种)
∴先将甲、乙2人站在两端,其余5人全排列,
得到:
| A | 2 2 |
| A | 5 5 |
(2)甲、乙、丙3人必须排在一起,
可先将甲、乙、丙3人捆绑在一起,再进行排列,
得到:
| A | 3 3 |
| A | 5 5 |
(3)甲不在排头且乙不在排尾,
先全排列,再排除甲在排头和乙在排尾的情况,
得到:
| A | 7 7 |
| A | 6 6 |
| A | 6 6 |
| A | 5 5 |
点评:本题是一道排列组合题,考查了特殊元素法、特殊位置法、淘汰法等方法,本题有一定的思维难度,计算量适中,属于中档题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知函数f(x)=a(x-
)-2lnx(a∈R),g(x)=-
,若至少存在一个x0∈[1,e],使f(x0)>g(x0)成立,则实数a的范围为( )
| 1 |
| x |
| a |
| x |
| A、[λ,+∞) |
| B、(0,+∞) |
| C、[0,+∞) |
| D、(G(x),+∞) |
函数y=x3-3x+1在x0处取极大值y0,而函数y=ax-1过点(x0,y0),则函数y=|ax-1|的增区间为( )
| A、(-∞,+∞) |
| B、(-∞,0) |
| C、(-∞,1) |
| D、(0,+∞) |
函数f(x)=
的定义域为R,则实数m的取值范围是( )
| -mx2-4mx-m+3 |
| A、[-1,0] |
| B、[-1,0) |
| C、(-∞,-1]∪(0,+∞) |
| D、(-∞,-1]∪[0,+∞) |
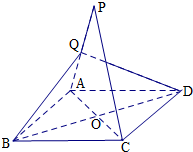 如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.
如图,P是菱形ABCD所在平面外一点,Q是PA中点,且QB=QD.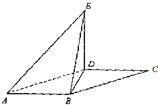 如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.
如图,平行四边形ABCD中,BD⊥AB,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD,证明:AB⊥面BDE.