题目内容
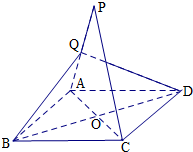如图，P是菱形ABCD所在平面外一点，Q是PA中点，且QB=QD．（1）求证：PC∥平面QBD；
（2）求证：平面QBD⊥平面PAC．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）首先利用中点得出中位线进一步证明线面平行
（2）利用菱形的性质进一步得到线线垂直，再利用线面垂直得到面面垂直．
（2）利用菱形的性质进一步得到线线垂直，再利用线面垂直得到面面垂直．
解答：
证明：（1）连结OQ，AC，BD
∵Q是PA中点，O是AC的中点
OQ∥PC
OQ?平面QBD，PC?平面QBD
所以PC∥平面QBD
（2）A在菱形ABCD中，AC⊥BD
在△QBD中，QB=QD，
∴OQ⊥BD
∴BD⊥平面PAC．
∵BD?平面QBD
∴平面QBD⊥平面PAC
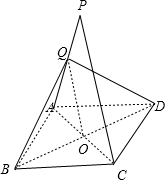
∵Q是PA中点，O是AC的中点
OQ∥PC
OQ?平面QBD，PC?平面QBD
所以PC∥平面QBD
（2）A在菱形ABCD中，AC⊥BD
在△QBD中，QB=QD，
∴OQ⊥BD
∴BD⊥平面PAC．
∵BD?平面QBD
∴平面QBD⊥平面PAC
点评：本题考查的知识要点：中位线定理，线面平行的判定定理，菱形的性质定理线面垂直的判定定理，面面垂直的判定定理．
练习册系列答案
相关题目
如图，在三棱锥A-BCD中，侧面ABD与底面BCD均为等腰三角形，∠BAD=∠BCD=90°，E为BD的中点，且AE⊥CE．不等式组
表示的平面区域的面积是（ ）
|
| A、30 | B、30.2 |
| C、30.25 | D、30.35 |
函数f（x）=xex-ex+1的单调递增区间是（ ）
| A、（-∞，e） |
| B、（1，e） |
| C、（e，+∞） |
| D、（e-1，+∞） |