题目内容
已知集合A={x|x2-1<0},B={x|x<m},若“a∈A”是“a∈B”的充分而不必要条件,则实数m的取值可以是( )
A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:解不等式x2-1<0可求出A,进而根据“a∈A”是“a∈B”的充分而不必要条件,得到A?B,进而得到m的取值范围,比较四个答案,可得结论.
解答:
解:解x2-1<0得:-1<x<1,
故集合A={x|x2-1<0}=(-1,1),
∵集合B={x|x<m},“a∈A”是“a∈B”的充分而不必要条件,
∴A?B,
故m≥1,
故选:C.
故集合A={x|x2-1<0}=(-1,1),
∵集合B={x|x<m},“a∈A”是“a∈B”的充分而不必要条件,
∴A?B,
故m≥1,
故选:C.
点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
某三棱锥的三视图如图所示,则该几何体的体积为( )
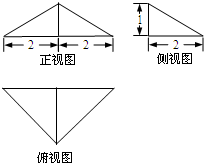

A、
| ||
B、
| ||
C、
| ||
| D、4 |
函数y=sin(2x-
)的一条对称轴为( )
| π |
| 6 |
A、x=-
| ||
B、x=
| ||
C、x=
| ||
D、x=-
|
已知下列四个命题:
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
;
④4条棱均为
的四面体的体积是
;
其中真命题的序号是( )
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
| 1 |
| 4 |
④4条棱均为
| 2 |
| 1 |
| 3 |
其中真命题的序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |