题目内容
已知函数f(x)=x2+2a1og2(x2+2)+a2-3有且只有一个零点,则实数a的值为( )
| A、1 | B、-3 | C、2 | D、1或-3 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:先确定函数f(x)是偶函数,再由函数f(x)的零点个数有且只有一个故只能是f(0)=0,从而得到答案.
解答:
解:∵函数f(x)=x2+2a1og2(x2+2)+a2-3,f(-x)=f(x),
∴f(x)为偶函数,
∴y=f(x)的图象关于y轴对称,由题意知f(x)=0只有x=0这一个零点,
把(0,0)代入函数表达式得:a2+2a-3=0,
解得:a=-3(舍),或a=1,
令t=x2,则f(x)=g(t)=t+2alog2(t+2)+a2-3.
当a=1时,g(t)=t+2log2(t+2)-2,
由于g(t)≥g(0)=0,当且仅当x=0时取等号,符合条件;
当a=-3时,g(t)=t-6log2(t+2)+6,
由g(30)=30-6×5+6>0,g(14)=14-6×4+6<0,
知f(x)至少有三个根,不符合.
所以,符合条件的实数a的值为1.
故答案选:A.
∴f(x)为偶函数,
∴y=f(x)的图象关于y轴对称,由题意知f(x)=0只有x=0这一个零点,
把(0,0)代入函数表达式得:a2+2a-3=0,
解得:a=-3(舍),或a=1,
令t=x2,则f(x)=g(t)=t+2alog2(t+2)+a2-3.
当a=1时,g(t)=t+2log2(t+2)-2,
由于g(t)≥g(0)=0,当且仅当x=0时取等号,符合条件;
当a=-3时,g(t)=t-6log2(t+2)+6,
由g(30)=30-6×5+6>0,g(14)=14-6×4+6<0,
知f(x)至少有三个根,不符合.
所以,符合条件的实数a的值为1.
故答案选:A.
点评:本题主要考查函数零点的概念,要注意函数的零点不是点,而是函数f(x)=0时的x的值,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知下列四个命题:
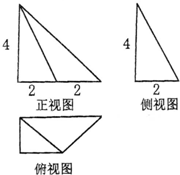
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
;
④4条棱均为
的四面体的体积是
;
其中真命题的序号是( )
①底面积和高均相等的柱体体积是锥体体积的3倍:
②正方体的截面是一个n边形,则n的最大值是6;
③在棱长为1的正方体ABCD-AB1C1D1中,三棱锥A1-ABC的体积是
| 1 |
| 4 |
④4条棱均为
| 2 |
| 1 |
| 3 |
其中真命题的序号是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
设已知a,b,m均为整数(m>0),若a和b被m除所得的余数相同,则称a和b对模m同余,记为a≡b(modm),若a=C
+C
•2+C
•22+…+C
•240,且a≡b(mod10),则b的值可以是( )
0 40 |
1 40 |
3 40 |
40 40 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
已知数列{an}满足:am=
(am-1+am+1)(m>1,m∈N),a4=4,则a3+a4+a5=( )
| 1 |
| 2 |
| A、4 | B、8 | C、12 | D、16 |
二次函数y=ax2+bx与指数函数y=(-
)x的图象只可能是( )
| b |
| a |
A、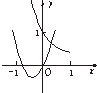 |
B、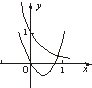 |
C、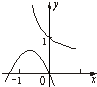 |
D、 |