题目内容
19.若关于x的不等式组$\left\{\begin{array}{l}{{x}^{3}+3{x}^{2}-x-3>0}\\{{x}^{2}-2ax-1≤0}\end{array}\right.$(a>0)的整数解有且仅有一个,则a的取值范围为( )| A. | [$\frac{3}{4}$,$\frac{4}{3}$] | B. | [$\frac{3}{4}$,$\frac{4}{3}$) | C. | ($\frac{3}{4}$,$\frac{4}{3}$) | D. | ($\frac{3}{4}$,$\frac{4}{3}$] |
分析 分别求出不等式的解,再根据整数解有且仅有一个,得到2≤a+$\sqrt{1+{a}^{2}}$<3,解得即可.
解答 解:由x3+3x2-x-3=x(x2-1)+3(x2-1)=(x2-1)(x+3)=(x+3)(x+1)(x-1)>0,解得-3<x<-1或x>1
由x2-2ax-1≤0,即(x-a)2≤1+a2,解得a-$\sqrt{1+{a}^{2}}$≤x≤a+$\sqrt{1+{a}^{2}}$,
∴-1<a-$\sqrt{1+{a}^{2}}$<0,a+$\sqrt{1+{a}^{2}}$>1
∵整数解有且仅有一个,
∴x=2,
∴2≤a+$\sqrt{1+{a}^{2}}$<3,
解得$\frac{3}{4}$≤a<$\frac{4}{3}$,
故选:B.
点评 本题考查了不等式的解法以及参数的取值范围,考查学生分析问题,解决问题的能力,属于中档题.

练习册系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x<0}\\{m-{x}^{2},x≥0}\end{array}\right.$,给出下列两个命题:
命题p:若m=$\frac{1}{4}$,则f(f(-1)=0.
命题q:?m∈(-∞,0),方程f(x)=0有解.
那么,下列命题为真命题的是( )
命题p:若m=$\frac{1}{4}$,则f(f(-1)=0.
命题q:?m∈(-∞,0),方程f(x)=0有解.
那么,下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
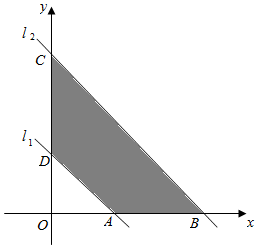 如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.
如图,已知直线l1:x+y-1=0,现将直线l1向上平移到直线l2的位置,若l2、l1和坐标轴围成的梯形面积为4,求l2的方程.