题目内容
11．
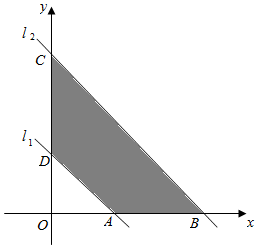如图，已知直线l1：x+y-1=0，现将直线l1向上平移到直线l2的位置，若l2、l1和坐标轴围成的梯形面积为4，求l2的方程．
分析 先求出l2和坐标轴围成的面积为$\frac{9}{2}$，再设直线l2：x+y-m=0，求出直线l2与x，y轴的交点坐标，表示出三角形的面积，求出m的值，从而求出直线l的方程即可．
解答 解：直线直线l1：x+y-1=0与坐标轴所围成的面积为$\frac{1}{2}$×1×1=$\frac{1}{2}$，
∵l2、l1和坐标轴围成的梯形面积为4，
∴l2和坐标轴围成的面积为$\frac{9}{2}$，
∵l2∥l1，
∴设直线l2：x+y-m=0，
当x=0，y=m，当y=0时，x=m，
∴$\frac{1}{2}$m2=$\frac{9}{2}$，
∴m=±3，
∵直线l1向上平移到直线l2的位置，
∴m=3，
∴l2的方程为x+y-3=0
点评 本题考查了求直线方程问题，考查直线的平行关系，三角形的面积问题，是一道中档题
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．设复数z=$\frac{1-i}{1+i}$（i为虚数单位），则z=（ ）
| A． | i | B． | -i | C． | 2i | D． | -2i |
2．已知a，b为空间两条不重合的直线，α，β为空间两个不重合的平面，则以下结论正确的是（ ）
| A． | 若α⊥β，a?α，则a⊥β | B． | 若α⊥β，a⊥β，则a∥α | C． | 若a?α，a∥β，则α∥β | D． | 若a?α，a⊥β，则α⊥β |
19．若关于x的不等式组$\left\{\begin{array}{l}{{x}^{3}+3{x}^{2}-x-3＞0}\\{{x}^{2}-2ax-1≤0}\end{array}\right.$（a＞0）的整数解有且仅有一个，则a的取值范围为（ ）
| A． | [$\frac{3}{4}$，$\frac{4}{3}$] | B． | [$\frac{3}{4}$，$\frac{4}{3}$） | C． | （$\frac{3}{4}$，$\frac{4}{3}$） | D． | （$\frac{3}{4}$，$\frac{4}{3}$] |