题目内容
有四个数和为21，前3个数为等比数列，后3个数为等差数列和为12，求这四个数．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：先根据题意设出这四个数，进而根据四个数和为21列出方程求得d，则四个数可得．
解答：
解：依题意可设这四个数分别为：
，4-d，4，4+d，则
由四个数和为21可列方程得，
+12=21
解得d=10或d=-2．
∴这四个数分别为：9，-6，4，14或9，6，4，2．
| (4-d)2 |
| 4 |
由四个数和为21可列方程得，
| (4-d)2 |
| 4 |
解得d=10或d=-2．
∴这四个数分别为：9，-6，4，14或9，6，4，2．
点评：本题主要考查了等差数列的性质和等比数列的性质．解题的关键是设出这四个数．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
若复数z满足
=2+i（其中i为虚数单位），则z的共轭复数为（ ）
| z+i |
| i |
| A、-1-i | B、1-i |
| C、-1+i | D、1+i |
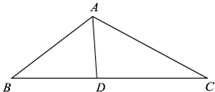若可变形的三角形模型在变换过程中三角形周长和面积可同时取得最小值（或最大值），则称此模型为“周积三角形”．某模型厂家用一根定长连接杆AD，两根单向伸缩连接杆AB、AC（A端固定，B、C端可伸缩）以及一根双向伸缩连接杆BC制作了如图所示的可变三角形模型（所有连接杆均为笔直的金属杆）．模型中，双向伸缩杆BC用一个活动连接装置固定在D点，使BC可在D处自由转动．已知：模型中，∠BAD=∠CAD=60°，AD=1分米，AB和AC最多可伸长到5分米，BC的双向伸缩能力均很强．设AB=x分米，AC=y分米．