题目内容
已知a＞0且a≠1，f（x）=
（1）求值：f（0）+f（1），f（-1）+f（2）；
（2）由（1）的结果归纳概括对所有实数x都成立的一个等式，并加以证明；
（3）若a∈N*，求和：f（-（n-1））+f（-（n-2））+…+f（-1）+f（0）+…f（n）．
| 1 | ||
ax+
|
（1）求值：f（0）+f（1），f（-1）+f（2）；
（2）由（1）的结果归纳概括对所有实数x都成立的一个等式，并加以证明；
（3）若a∈N*，求和：f（-（n-1））+f（-（n-2））+…+f（-1）+f（0）+…f（n）．
考点：数学归纳法,函数的值
专题：计算题,函数的性质及应用
分析：（1）直接代入，即可求值；
（2）由（1）归纳f（x）+f（1-x）=
，再进行证明；
（3）利用倒序相加法，即可求解．
（2）由（1）归纳f（x）+f（1-x）=
| ||
| a |
（3）利用倒序相加法，即可求解．
解答：
解：（1）f（0）+f（1）=
+
=
=
，
f（-1）+f（2）=
+
=
=
；
（2）由（1）归纳f（x）+f（1-x）=
，证明如下：
f（x）+f（1-x）=
+
=
+
=
，
（3）S=f（-（n-1））+f（-（n-2））+…+f（-1）+f（0）+…f（n）
∴Sf（n）+f（n-1））+…+f（-（n-1）+f（-（n-2））．
两式相加可得2S=2n•
，
∴S=
．
| 1 | ||
1+
|
| 1 | ||
a+
|
| 1 | ||
|
| ||
| a |
f（-1）+f（2）=
| 1 | ||
a-1+
|
| 1 | ||
a2+
|
| 1 | ||
|
| ||
| a |
（2）由（1）归纳f（x）+f（1-x）=
| ||
| a |
f（x）+f（1-x）=
| 1 | ||
ax+
|
| 1 | ||
a1-x+
|
| 1 | ||
ax+
|
| ax | ||||
|
| ||
| a |
（3）S=f（-（n-1））+f（-（n-2））+…+f（-1）+f（0）+…f（n）
∴Sf（n）+f（n-1））+…+f（-（n-1）+f（-（n-2））．
两式相加可得2S=2n•
| ||
| a |
∴S=
n
| ||
| a |
点评：本题考查函数值的求法，解题时要认真审题，仔细解答，注意函数性质的合理运用．
练习册系列答案
相关题目
两条不同的直线l1，l2平行的一个充分不必要条件是（ ）
| A、l1，l2都平行于同一个平面 |
| B、l1，l2与同一个平面所成的角相等 |
| C、l1平行于l2所在的平面 |
| D、l1，l2都垂直于同一个平面 |
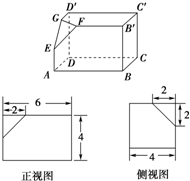如图所示的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm）．