题目内容
设等差数列{an}的前n项和为Sn,a4=S2,a2n+2=2an,
(1)求数列{an}的通项公式;
(2)若bn=
,求数列{bn}的前n项和Tn,并求Tn的取值范围.
(1)求数列{an}的通项公式;
(2)若bn=
| 4 |
| anan+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式求出a1=4,d=2,由此能求出an=2n+2.
(2)由bn=
=
=
-
,利用裂项求和法能求出
≤Tn<
.
(2)由bn=
| 4 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 6 |
| 1 |
| 2 |
解答:
解:(1)∵等差数列{an}的前n项和为Sn,a4=S2,a2n+2=2an,
∴
,
解得a1=4,d=2,
∴an=4+(n-1)×2=2n+2.
(2)bn=
=
=
-
,
∴Tn=
-
+
-
+…+
-
=
-
,
∴Tn<
,又Tn=
-
是增函数,∴(Tn)min=T1=
-
=
,
∴
≤Tn<
.
∴
|
解得a1=4,d=2,
∴an=4+(n-1)×2=2n+2.
(2)bn=
| 4 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
∴Tn<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 1+2 |
| 1 |
| 6 |
∴
| 1 |
| 6 |
| 1 |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
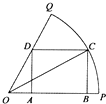 如图,已知OPQ是半径为
如图,已知OPQ是半径为