题目内容
仔细观察下面的不等式,寻找规律,合理猜想出第n个不等式,并用数学归纳法证明你的猜想.
(1+
)>
,(1+
)(1+
)>
,(1+
)(1+
)(1+
)>
,(1+
)(1+
)(1+
)(1+
)>
,(1+
)(1+
)(1+
)(1+
)(1+
)>
.…
(1+
| 1 |
| 1 |
| 3 |
| 1 |
| 1 |
| 1 |
| 3 |
| 5 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 7 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 9 |
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 9 |
| 11 |
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:观察所给不等式,注意不等式的左边与右边的特征,得到猜想,然后利用数学归纳法的证明标准,验证n=1时成立,假设n=k是成立,证明n=k+1时等式也成立即可.
解答:
解:猜想:(1+
)(1+
)(1+
)•…•(1+
)>
…(3分)
证明:(1)n=1时,不等式显然成立.…(4分)
(2)假设n=k时,不等式成立,即(1+
)(1+
)•…•(1+
)>
成立,
当n=k+1时,
不等式的左边=(1+
)(1+
)•…•(1+
)(1+
)>
(1+
)…(4分)
下面证明:
(1+
)≥
,由于这个不等式的两边都是正数,只要证明(2k+1)(1+
)2≥2k+3即可.
而(2k+1)(1+
)2=(2k+1)(1+
+
)>(2k+1)(1+
)=(2k+1)
=2k+3.故n=k+1时不等式成立.
综合(1)和(2)知原不等式对一切正整数成立.…(14分)
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 2n+1 |
证明:(1)n=1时,不等式显然成立.…(4分)
(2)假设n=k时,不等式成立,即(1+
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
| 2k+1 |
当n=k+1时,
不等式的左边=(1+
| 1 |
| 1 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
| 1 |
| 2k+1 |
| 2k+1 |
| 1 |
| 2k+1 |
下面证明:
| 2k+1 |
| 1 |
| 2k+1 |
| 2k+3 |
| 1 |
| 2k+1 |
而(2k+1)(1+
| 1 |
| 2k+1 |
| 2 |
| 2k+1 |
| 1 |
| (2k+1)2 |
| 2 |
| 2k+1 |
| 2k+3 |
| 2k+1 |
综合(1)和(2)知原不等式对一切正整数成立.…(14分)
点评:本题考查归纳推理,用数学归纳法证明等式,证明故当n=k+1时,猜想也成立,是解题的难点和关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
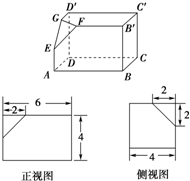 如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).