题目内容
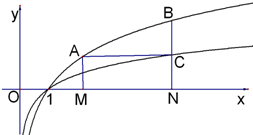 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.(1)当a=2,b=4,c=3时,求实数m的值;
(2)当b=a2时,求
| m |
| b |
| 2c |
| a |
(3)已知h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)内任意两个变量,且x1<x2,求证:h[f(x2)]<φ[f(x1)].
考点:函数与方程的综合运用,对数函数的图像与性质
专题:函数的性质及应用
分析:(1)通过a=2,b=4,c=3时,求出ABC坐标,利用AC与x轴平行,列出方程,即可求实数m的值;
(2)通过ABC坐标,利用平行关系得到方程,通过当b=a2时,化简
-
为二次函数的形式,即可求解表达式的最小值;
(3)通过h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)内任意两个变量,且x1<x2,利用对数函数的单调性,以及对数的运算法则,即可证明:h[f(x2)]<φ[f(x1)].
(2)通过ABC坐标,利用平行关系得到方程,通过当b=a2时,化简
| m |
| b |
| 2c |
| a |
(3)通过h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)内任意两个变量,且x1<x2,利用对数函数的单调性,以及对数的运算法则,即可证明:h[f(x2)]<φ[f(x1)].
解答:
(1)解:由题意得A(2,log32),B(4,log34),C(4,logm4)
因为AC与x轴平行
所以logm4=log32
所以m=9
(2)解:由题意得A(a,logca),B(b,logcb),C(b,logmb)
因为AC与x轴平行
所以logmb=logca
因为b=a2,所以m=c2
所以
-
=
-
=(
-1)2-1
所以
=1时,达到最小值-1
(3)证明:因为a<x1<x2<b,且c>1
所以logca<logcx1<logcx2<logcb
又因为a>1,b>1
所以alogcx2<alogcb,blogca<blogcx1
又因为logcblogca=logcalogcb
所以logcalogcb=logcblogca
所以alogcb=blogca
所以alogcx2<blogcx1
即h[f(x2)]<φ[f(x1)].
因为AC与x轴平行
所以logm4=log32
所以m=9
(2)解:由题意得A(a,logca),B(b,logcb),C(b,logmb)
因为AC与x轴平行
所以logmb=logca
因为b=a2,所以m=c2
所以
| m |
| b |
| 2c |
| a |
| c2 |
| a2 |
| 2c |
| a |
| c |
| a |
所以
| c |
| a |
(3)证明:因为a<x1<x2<b,且c>1
所以logca<logcx1<logcx2<logcb
又因为a>1,b>1
所以alogcx2<alogcb,blogca<blogcx1
又因为logcblogca=logcalogcb
所以logcalogcb=logcblogca
所以alogcb=blogca
所以alogcx2<blogcx1
即h[f(x2)]<φ[f(x1)].
点评:本题考查复合函数的单调性,对数的运算性质,考查函数与方程的综合应用,是中档题.

练习册系列答案
相关题目
在(x-y)10的展开式中,系数最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
“lgx,lgy,lgz成等差数列”是“y2=xz”成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
i是虚数单位,复数(1-i)2的虚部为( )
| A、-2 | B、2 | C、-2i | D、2i |
直线x+
y=0被圆x2+y2-4y=0所截得的弦长为( )
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|