题目内容
已知数列{an}满足:a1=a,an+1=
an2-an+2,其中n∈N*.
(Ⅰ)是否存在实数a使得{an}为等差数列,若存在,求出a的值,若不存在,请说明理由;
(Ⅱ)当a=4时,证明:
+
+…+
<
.
| 1 |
| 2 |
(Ⅰ)是否存在实数a使得{an}为等差数列,若存在,求出a的值,若不存在,请说明理由;
(Ⅱ)当a=4时,证明:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)an+1-an=
an2-2an+2=
(an-2)2,若{an}为等差数列,则公差为0,从而an=2,由此求出a=2.
(Ⅱ)由an+1-2=
an2-an=
an(an-2),得
=
=
-
,由此能证明
+
+…+
<
.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由an+1-2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| an+1-2 |
| 1 | ||
|
| 1 |
| an-2 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
解答:
(本小题满分12分)
(Ⅰ)解:an+1-an=
an2-2an+2=
(an-2)2,
若{an}为等差数列,
则
(an-2)2为常数,
即an为常数,
从而公差为0,∴an=2,
此时{an}为常数列,是等差数列,
所以存在a=2满足题意.…(4分)
(Ⅱ)证明:an+1-2=
an2-an=
an(an-2),
则
=
=
-
,
∴
=
-
,
∴
+
+…+
=
-
=
-
an+1-an=
(an-2)2,
∵a1≠2∴an≠2,
∴an+1-an>0数列{an}单增,
∴an+1>a1=4,
∴
+
+…+
<
.…(12分)
(Ⅰ)解:an+1-an=
| 1 |
| 2 |
| 1 |
| 2 |
若{an}为等差数列,
则
| 1 |
| 2 |
即an为常数,
从而公差为0,∴an=2,
此时{an}为常数列,是等差数列,
所以存在a=2满足题意.…(4分)
(Ⅱ)证明:an+1-2=
| 1 |
| 2 |
| 1 |
| 2 |
则
| 1 |
| an+1-2 |
| 1 | ||
|
| 1 |
| an-2 |
| 1 |
| an |
∴
| 1 |
| an |
| 1 |
| an-2 |
| 1 |
| an+1-2 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| a1-2 |
| 1 |
| an+1-2 |
| 1 |
| 2 |
| 1 |
| an+1-2 |
| 1 |
| 2 |
∵a1≠2∴an≠2,
∴an+1-an>0数列{an}单增,
∴an+1>a1=4,
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| 2 |
点评:本题考查使数列为等差数列的实数值的求法,考查不等式的证明,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在(x-y)10的展开式中,系数最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
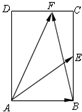 如图,在矩形ABCD中,AB=2,BC=2
如图,在矩形ABCD中,AB=2,BC=2