题目内容
求函数y=log
的最小值.
| 1 |
| 2 |
| 1 |
| x2-2x+5 |
考点:对数函数的图像与性质
专题:计算题
分析:令g(x)=x2-2x+5,先求出g(x)min=4,则
max=
,由对数函数的图象和性质即可求解.
| 1 |
| g(x) |
| 1 |
| 4 |
解答:
解:令g(x)=x2-2x+5,显然g(x)=(x-1)2+4有最小值g(x)min=4,
故
max=
,
又因为y=log
在(0,+∞)上是单调递减的,故当
max取最大值
时,y=log
取最小值,
由对数函数的图象和性质可知,ymin=2.
故y=log
的最小值是2.
故
| 1 |
| g(x) |
| 1 |
| 4 |
又因为y=log
| 1 |
| 2 |
| 1 |
| g(x) |
| 1 |
| g(x) |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| g(x) |
由对数函数的图象和性质可知,ymin=2.
故y=log
| 1 |
| 2 |
| 1 |
| x2-2x+5 |
点评:本题主要考察了对数函数的图象与性质,属于基础题.

练习册系列答案
相关题目
下列说法正确的个数是( )
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
①平行于同一直线的两条直线平行
②平行于同一平面的两个平面平行
③两条平行线中的一条和一个平面平行,则另一条也与这个平面平行
④一条直线与两个平行平面中的一个平面平行,则这条直线与另一平面也平行.
| A、1 | B、2 | C、3 | D、4 |
在平面直角坐标系xOy上的区域D由不等式|x+2|+|y+2|≤2给定.则区域D的面积等于( )
| A、2 | ||
| B、4 | ||
C、4
| ||
| D、8 |
已知{an}是公差不为0的等差数列,a1=2且a2,a4,a8成等比数列,若bn=
,则数列{bn}的前n项和的取值范围是( )
| 2 |
| n(an+2) |
A、[
| ||
| B、(0,1) | ||
C、(0,
| ||
| D、(1,+∞) |
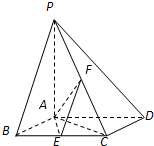 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.
在正方体ABCD-A1B1C1D1中,AA1=2,E为棱CC1的中点.