题目内容
已知{an}是公差不为0的等差数列,a1=2且a2,a4,a8成等比数列,若bn=
,则数列{bn}的前n项和的取值范围是( )
| 2 |
| n(an+2) |
A、[
| ||
| B、(0,1) | ||
C、(0,
| ||
| D、(1,+∞) |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:设等差数列{an}是公差为d且d不为0,由题意和等比中项的性质列出方程求出d的值,代入等差数列的通项公式求出an,再代入bn=
化简后进行裂项,由裂项相消法求出数列{bn}的前n项和,化简后由式子个特点和n的取值范围求出它的范围.
| 2 |
| n(an+2) |
解答:
解:设等差数列{an}是公差为d,且d不为0,
由a1=2且a2,a4,a8成等比数列得,(2+4d)2=(2+d)(2+7d),
解得d=2或d=0(舍去),
所以an=a1+(n-1)d=2n,
则bn=
=
=
-
,
所以数列{bn}的前n项和Sn=b1+b2+…+bn
=(1-
)+(
-
)+…+(
-
)=1-
<1,
又n≥1,所以Sn≥
,
所以数列{bn}的前n项和Sn的取值范围是[
,1),
故选:A.
由a1=2且a2,a4,a8成等比数列得,(2+4d)2=(2+d)(2+7d),
解得d=2或d=0(舍去),
所以an=a1+(n-1)d=2n,
则bn=
| 2 |
| n(an+2) |
| 2 |
| n(2n+2) |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
所以数列{bn}的前n项和Sn=b1+b2+…+bn
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
又n≥1,所以Sn≥
| 1 |
| 2 |
所以数列{bn}的前n项和Sn的取值范围是[
| 1 |
| 2 |
故选:A.
点评:本题考查了等比中项的性质,等差数列的通项公式,数列的求和方法:裂项相消法的应用,以及数列的函数特性.

练习册系列答案
相关题目
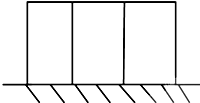 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y(1)请把y表示成x的函数;
(2)当x为何值时,函数取最大值,并求出最大值.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0,m∈R,当直线l被圆C截得的弦长最短时的m的值是( )
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
 如图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计:
如图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计: