题目内容
设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2
(1)设bn=an+1-2an,证明数列{bn}是等比数列;
(2)令cn=
,求cn及数列an.
(1)设bn=an+1-2an,证明数列{bn}是等比数列;
(2)令cn=
| an |
| 2n-1 |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)依题意,可求得b1=a2-2a1=3,an+2-2an+1=2(an+1-2an),即bn+1=2bn,从而可证数列{bn}为等比数列;
(2)由(1)知等比数列{bn}中b1=3,公比q=2,可求得
-
=
,知数列{
}是首项为
,公差为
的等差数列,于是可求得
=
+(n-1)×
=
n-
,而Cn=
,于是可求Cn及an.
(2)由(1)知等比数列{bn}中b1=3,公比q=2,可求得
| an+1 |
| 2n+1 |
| an |
| 2n |
| 3 |
| 4 |
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| an |
| 2n-1 |
解答:
证明:(1)由已知有a1+a2=4a1+2,解得a2=3a1+2=5,
故b1=a2-2a1=3,
又an+2=Sn+2-Sn+1=4an+1+2-(4an+2)=4an+1-4an,
于是an+2-2an+1=2(an+1-2an),即bn+1=2bn,
因此数列{bn}是首项为3,公比为2的等比数列.
(2)由(1)知等比数列{bn}中b1=3,公比q=2,
所以an+1-2an=3×2n-1,于是
-
=
,
因此数列{
}是首项为
,公差为
的等差数列,
=
+(n-1)×
=
n-
,
∴Cn=
=
=2(
n-
)=
n-
,
∴an=(3n-1)•2n-2.
故b1=a2-2a1=3,
又an+2=Sn+2-Sn+1=4an+1+2-(4an+2)=4an+1-4an,
于是an+2-2an+1=2(an+1-2an),即bn+1=2bn,
因此数列{bn}是首项为3,公比为2的等比数列.
(2)由(1)知等比数列{bn}中b1=3,公比q=2,
所以an+1-2an=3×2n-1,于是
| an+1 |
| 2n+1 |
| an |
| 2n |
| 3 |
| 4 |
因此数列{
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
∴Cn=
| an |
| 2n-1 |
| 2an |
| 2n |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
∴an=(3n-1)•2n-2.
点评:本题考查数列递推关系的应用与等比关系的确定,由bn=an+1-2an=3×2n-1,得到
-
=
是关键,考查转化思想与运算能力,属于中档题.
| an+1 |
| 2n+1 |
| an |
| 2n |
| 3 |
| 4 |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
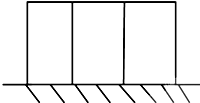 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y(1)请把y表示成x的函数;
(2)当x为何值时,函数取最大值,并求出最大值.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0,m∈R,当直线l被圆C截得的弦长最短时的m的值是( )
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
