Question

在正方体ABCD-A₁B₁C₁D₁中，AA₁=2，E为棱CC₁的中点．
（1）求三棱锥E-ABD的体积；
（2）求证：B₁D₁⊥AE；
（3）求证：AC∥平面B₁DE．

Answer 1

考点：直线与平面垂直的性质,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离,空间角

分析：（1）直接利用棱锥的体积的公式求的结果．
（2）要证线线垂直，通过线面垂直进行转化．
（3）通过做平面B₁DE的延展面，通过线面平行的判定来进行证明．

解答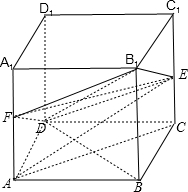： （1）解：在正方体ABCD-A₁B₁C₁D₁中，AA₁=2，E为棱CC₁的中点．
∴CE=1
则：VE-ABD=

1

3

S△ABD•CE=

2

3

（2）证明：在正方体中，CE⊥平面ABCD
∴CE⊥BD
在正方形ABCD中，AC⊥BD
∴BD⊥平面ACE
∵B₁D₁∥BD
∴B₁D₁⊥平面ACE
∴B₁D₁⊥AE
（3）证明：在侧棱AA₁上取中点F，连结DF，B₁F，EF
由于E、F分别是侧棱A₁A和C₁C的中点
所以：DF∥B₁E
∴D、F、B₁、E四点共面
∴AC∥EF
AC?平面B₁EDF  EF?平面B₁EDF
∴AC∥平面B₁EDF
平面B₁EDF和平面B₁DE重合∴
∴AC∥平面B₁DE．

点评：本题考查的知识要点：棱锥的体积，线面垂直的性质与判定，线面平行的判定定理，重点考查空间想象能力和转化能力．