题目内容
3.已知数列{an}为等差数列,且a4=9,a9=-6.(1)求通项an;
(2)求a12的值.
分析 (1)利用等差数列通项公式列出方程组,求出首项与公差,由此能求出通项an.
(2)由通项通项an,能求出a12的值.
解答 解:(1)∵数列{an}为等差数列,且a4=9,a9=-6,
∴$\left\{\begin{array}{l}{{a}_{1}+3d=9}\\{{a}_{1}+8d=-6}\end{array}\right.$,解得a1=18,d=-3,
∴通项an=18+(n-1)×(-3)=21-3n.
(2)a12=21-3×12=-15.
点评 本题考查等差数列的通项公式和第12项和求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
13.sin2(π+α)-cos(π-α)•cosα+1=( )
| A. | 2 | B. | 1 | C. | 2sin2α | D. | 0 |
11.已知函数f(x)=(x-a)2+(ex-a)2(a∈R),若存在x0∈R,使得f(x0)≤$\frac{1}{2}$成立,则实数a的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{2}$ |
18.在△ABC中,a2+b2+c2=2$\sqrt{3}$bcsinA,则△ABC的形状是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
1.设a,b∈R,定义:M(a,b)=$\frac{a+b+|a-b|}{2}$,m(a,b)=$\frac{a+b-|a-b|}{2}$.下列式子错误的是( )
| A. | M(a,b)+m(a,b)=a+b | B. | m(|a+b|,|a-b|)=|a|-|b| | C. | M(|a+b|,|a-b|)=|a|+|b| | D. | m(M(a,b),m(a,b))=m(a,b) |
6.化简:$\overrightarrow{AB}$+$\overrightarrow{OA}$-$\overrightarrow{OB}$=( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{BA}$ | C. | 2$\overrightarrow{AB}$ | D. | -2$\overrightarrow{AB}$ |
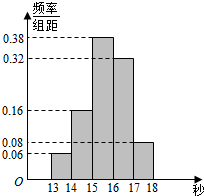 某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.
某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.