题目内容
13.某家具厂生产一种课桌,每张课桌的成本为50元,出厂单价定为80元,该厂为鼓励销售商多订购,决定一次订购量超过100张时,每超过一张,这批订购的全部课桌出厂单价降低0.02元.根据市场调查,销售商一次订购量不会超过1000张.(Ⅰ)设一次订购量为x张,课桌的实际出厂单价为P元,求P关于x的函数关系式P(x);
(Ⅱ)当一次订购量x为多少时,该家具厂这次销售课桌所获得的利润f(x)最大?其最大利润是多少元?(家具厂售出一张课桌的利润=实际出厂单价-成本).
分析 (1)当0<x≤100时,P=80;当100<x≤1000时,P=80-0.02(x-100),由此可得分段函数;
(2)利用工厂售出一个零件的利润=实际出厂单价-成本,即可求出当销售商一次订购了800个零件时,该厂获得的利润.
解答 解:(Ⅰ)根据题意得:P(x)=$\left\{\begin{array}{l}{80,}&{0<x≤100,x∈N}\\{80-0.02(x-100),}&{100<x≤1000,x∈N}\end{array}\right.$;(4分)
即P(x)=$\left\{\begin{array}{l}{80,}&{0<x≤100,x∈N}\\{82-0.02x,}&{100<x≤1000,x∈N}\end{array}\right.$ (5分)
(Ⅱ)由(Ⅰ)得f(x)=$\left\{\begin{array}{l}{(80-50)x,}&{0<x≤100,x∈N}\\{(82-0.02x-50)x,}&{100<x≤1000,x∈N}\end{array}\right.$ (7分)
即f(x)=$\left\{\begin{array}{l}{30x,}&{0<x≤100,x∈N}\\{32x-0.02{x}^{2},}&{100<x≤1000.x∈N}\end{array}\right.$ (8分)
(ⅰ)当0<x≤100,
则x=100时,f(x)max=f(100)=3000 (9分)
(ⅱ)当100<x≤1000,
则x=800时,f(x)max=f(800)=32×800-0.02×8002=12800 (11分)
∵12800>3000,
∴x=800时,f(x)有最大值,其最大值为12800元.
答:当一次订购量为800张时,该家具厂在这次订购中所获得的利润最大,其最大利润是12800元.(12分)
点评 本题主要考查函数的应用问题,根据条件建立分段函数是解决本题的关键.考查应用数学知识分析问题和解决问题的能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{2}$ |
| A. | M(a,b)+m(a,b)=a+b | B. | m(|a+b|,|a-b|)=|a|-|b| | C. | M(|a+b|,|a-b|)=|a|+|b| | D. | m(M(a,b),m(a,b))=m(a,b) |
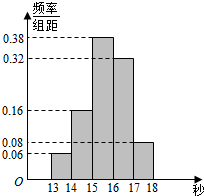 某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.
某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.