题目内容
17.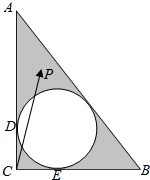 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
分析 求出内切圆半径,根据三点共线原理得出x+y分别对于1,2,4,8时P点的轨迹,从而判断出答案.
解答  解:设圆心为O,半径为r,则OD⊥AC,OE⊥BC,∴3-r+4-r=5,解得r=1.
解:设圆心为O,半径为r,则OD⊥AC,OE⊥BC,∴3-r+4-r=5,解得r=1.
连结DE,则当x+y=1时,P在线段DE上,排除A;
在AC上取点M,在CB上取点N,使得CM=2CD,CN=2CE,连结MN,∴$\overrightarrow{CP}$=$\frac{x}{2}$$\overrightarrow{CM}$+$\frac{y}{2}$$\overrightarrow{CN}$.
则点P在线段MN上时,$\frac{x}{2}$+$\frac{y}{2}$=1,故x+y=2.
同理,当x+y=4或x+y=8时,P点不在三角形内部.排除C,D.
故选:B.
点评 本题考查了平面向量的基本定理,三点共线原理,属于中档题.

练习册系列答案
相关题目
9.如果f(x)在[-5,5]上是奇函数,且f(3)<f(1),则( )
| A. | f(-1)<f(-3) | B. | f(0)>f(1) | C. | f(-1)<f(1) | D. | f(-3)<f(-5) |
6.化简:$\overrightarrow{AB}$+$\overrightarrow{OA}$-$\overrightarrow{OB}$=( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{BA}$ | C. | 2$\overrightarrow{AB}$ | D. | -2$\overrightarrow{AB}$ |
7.下列关于函数f(x)=sinx(cosx+sinx)的说法中,不正确的是( )
| A. | f(x)的最小正周期为π | |
| B. | f(x)的图象关于直线x=-$\frac{π}{8}$对称 | |
| C. | f(x)的图象关于点($\frac{π}{8}$,0)对称 | |
| D. | f(x)的图象向右平移$\frac{π}{8}$后得到一个偶函数的图象 |
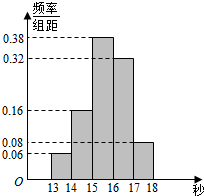 某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.
某班50名学生在一次百米测试中,成绩全部在13秒与18秒之间,大于或等于14秒的为良好,由测试结果得到的频率分布直方图如图,则该班百米测试中成绩良好的人数有人47.