题目内容
已知数列{an}的前n项和为Sn,且Sn=
(an-1).
(I)求数列{an}的通项公式;
(Ⅱ)设bn=log3a1+log3a2+…+log3an,求数列{
}的前n项和Tn.
| 3 |
| 2 |
(I)求数列{an}的通项公式;
(Ⅱ)设bn=log3a1+log3a2+…+log3an,求数列{
| 1 |
| bn |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由Sn=
(an-1),利用S1=a1,an=Sn-Sn-1,推导出{an}是首项为3,公比为3的等比数列,由此能求出an.
(Ⅱ)由an=3n,bn=log3a1+log3a2+…+log3an,推导出
=2(
-
),由此利用裂项求和法能求出数列{
}的前n项和Tn.
| 3 |
| 2 |
(Ⅱ)由an=3n,bn=log3a1+log3a2+…+log3an,推导出
| 1 |
| bn |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| bn |
解答:
解:(Ⅰ)∵数列{an}的前n项和为Sn,且Sn=
(an-1),
∴当n=1时,S1=a1=
(a1-1),解得a1=3,
当n≥2时,an=Sn-Sn-1=
(an-1)-
(an-1-1)
=
an-
an-1,
整理,得an=3an-1,
∴{an}是首项为3,公比为3的等比数列,
∴an=3×3n-1=3n.
(Ⅱ)∵an=3n,
∴bn=log3a1+log3a2+…+log3an
=1+2+3+…+n
=
,
∴
=
=2(
-
),
∴Tn=2[(1-
)+(
-
)+…+(
-
)]
=2(1-
)
=
.
| 3 |
| 2 |
∴当n=1时,S1=a1=
| 3 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| 3 |
| 2 |
| 3 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
整理,得an=3an-1,
∴{an}是首项为3,公比为3的等比数列,
∴an=3×3n-1=3n.
(Ⅱ)∵an=3n,
∴bn=log3a1+log3a2+…+log3an
=1+2+3+…+n
=
| n(n-1) |
| 2 |
∴
| 1 |
| bn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=2(1-
| 1 |
| n+1 |
=
| 2n |
| n+1 |
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列结论中,正确的是( )
| A、“?x∈Q,x2-5=0”的否定是假命题 |
| B、“?x∈R,x2+1<1”的否定是“?x∈R,x2+1<1” |
| C、“2≤2”是真命题 |
| D、“?x∈R,x2+1≠0”的否定是真命题 |
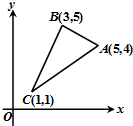 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是