题目内容
在数列{an}中an+1=2an+2n+1（n∈N*），a1=2，
（1）求证：数列{
}是等差数列，并求数列{an}的通项公式；
（2）求数列{an}前n项和Sn．
（1）求证：数列{
| an |
| 2n |
（2）求数列{an}前n项和Sn．
考点：数列的求和
专题：等差数列与等比数列
分析：（1）由题设条件推导出
-
=1，由此能证明数列{
}是等差数列，并能求出数列{an}的通项公式
．
（2）由an=n•2n，由错位相减法能求出{an}前n项和Sn．
| an+1 |
| 2n+1 |
| an |
| 2n |
| an |
| 2n |
．
（2）由an=n•2n，由错位相减法能求出{an}前n项和Sn．
解答：
解：（1）在数列{an}中，
∵an+1=2an+2n+1（n∈N*），a1=2，
∴
=
+1，∴
-
=1，…（2分）
∴数列{
}是以
=1为首项，1为公差的等差数列，…（4分）
=1+(n-1)=n，
∴an=n•2n．…（6分）
（2）∵an=n•2n，
∴Sn=1×2+2×22+3×23+…+n•2n，…①
2Sn=1×22+2×23+…+（n-1）•2n+n•2n+1，…②…（8分）
由①-②，得-Sn=2+22+23+…+2n-n•2n+1
=
-n•2n+1
=2n+1-2-n•2n+1，…（10分）
∴Sn=(n-1)•2n+1+2．…（12分）
∵an+1=2an+2n+1（n∈N*），a1=2，
∴
| an+1 |
| 2n+1 |
| an |
| 2n |
| an+1 |
| 2n+1 |
| an |
| 2n |
∴数列{
| an |
| 2n |
| a1 |
| 2 |
| an |
| 2n |
∴an=n•2n．…（6分）
（2）∵an=n•2n，
∴Sn=1×2+2×22+3×23+…+n•2n，…①
2Sn=1×22+2×23+…+（n-1）•2n+n•2n+1，…②…（8分）
由①-②，得-Sn=2+22+23+…+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
=2n+1-2-n•2n+1，…（10分）
∴Sn=(n-1)•2n+1+2．…（12分）
点评：本题考查等差数列的证明，考查数列的通项公式的求法，考查数列的通项公式的求法，是中档题．
练习册系列答案
相关题目
设a，b∈R，则“（a-b）a2＞0”是“a＞b”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
已知变量x，y满足约束条件
，若x+2y≥-5恒成立，则实数a的取值范围为（ ）
|
| A、（-∞，-1] |
| B、[-1，+∞） |
| C、[-1，1] |
| D、[-1，1） |
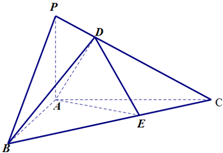如图，在△ABC中，∠BAC=90°，AC=2AB，PA垂直△ABC所在的平面，PC与△ABC所在的平面成30°角，点D在线段PC上，点E在线段BC上．
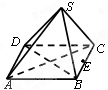如图，正四棱锥S-ABCD中，AB=2，E是边BC的中点，动点P在四棱锥的表面上运动，且总保持