题目内容
已知圆x2+y2+mx-
=0与抛物线y=
x2的准线相切,则m= .
| 1 |
| 4 |
| 1 |
| 4 |
考点:圆与圆锥曲线的综合
专题:计算题
分析:先求抛物线的准线方程,再确定圆x2+y2+mx-
=0的圆心与半径,利用圆x2+y2+mx-
=0与抛物线y=
x2的准线相切,建立方程,从而得解.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:抛物线y=
x2可化为:x2=4y
∴抛物线的准线方程是y=-1,
圆x2+y2+mx-
=0的圆心是(-
,0),半径r=
,
∵圆x2+y2+mx-
=0与抛物线y=
x2的准线相切,
∴根据圆心到直线的距离等于半径可得
=1
∴m=±
故答案为:±
| 1 |
| 4 |
∴抛物线的准线方程是y=-1,
圆x2+y2+mx-
| 1 |
| 4 |
| m |
| 2 |
| ||
| 2 |
∵圆x2+y2+mx-
| 1 |
| 4 |
| 1 |
| 4 |
∴根据圆心到直线的距离等于半径可得
| ||
| 2 |
∴m=±
| 3 |
故答案为:±
| 3 |
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力,属于中档题.

练习册系列答案
相关题目
多项式1-a2-b2+2ab分解因式的结果是( )
| A、(1-a-b)(1+a+b) |
| B、(1+a-b)(1-a+b) |
| C、(a+b+1)(a-b-1) |
| D、-(a-b+1)(a+b-1) |
抛物线y2=2px(p>0)的焦点到双曲线
-
=1渐近线的距离为
,则实数p等于( )
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
| A、2 | B、4 | C、8 | D、16 |
已知直线y=ex+1与曲线y=ex+a相切(e是自然对数的底数),则a的值是( )
| A、e | ||
B、
| ||
| C、e+1 | ||
| D、1 |
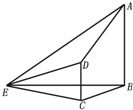 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.