题目内容
以下结论中,正确结论的序号为 .
①过平面α外一点P,有且仅有一条直线与α平行;②过平面α外一点P,有且仅有一个平面与α平行;
③过直线l外一点P,有且仅有一条直线与l平行;④过直线l外一点P,有且仅有一个平面与l平行;
⑤与两个相交平面的交线平行的直线必与两相交平面都平行;
⑥过空间内任意一点有且仅有一个平面与两条异面直线都平行;
⑦过空间内任意一点有且仅有一条直线与两条异面直线都相交.
①过平面α外一点P,有且仅有一条直线与α平行;②过平面α外一点P,有且仅有一个平面与α平行;
③过直线l外一点P,有且仅有一条直线与l平行;④过直线l外一点P,有且仅有一个平面与l平行;
⑤与两个相交平面的交线平行的直线必与两相交平面都平行;
⑥过空间内任意一点有且仅有一个平面与两条异面直线都平行;
⑦过空间内任意一点有且仅有一条直线与两条异面直线都相交.
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①过平面α外一点P,有无数条直线与α平行,故①错误;
②过平面α外一点P,有且仅有一个平面与α平行,
由平面与平面平行的判定定理得②正确;
③过直线l外一点P,有且仅有一条直线与l平行,由平行公理得③正确;
④过直线l外一点P,有无数个平面与l平行,故④错误;
⑤与两个相交平面的交线平行的直线与两相交平面都平行或包含于一个平面中,故⑤错误;
⑥过空间内任意一点有且仅有一个平面与两条异面直线都平行,
当空间这一点在两条异面直线的一条上,不成立,故⑥错误;
⑦过空间内任意一点有且仅有一条直线与两条异面直线都相交,
当点在两条异面直线的一条直线上时,不成立,故⑦错误.
故答案为:②③.
②过平面α外一点P,有且仅有一个平面与α平行,
由平面与平面平行的判定定理得②正确;
③过直线l外一点P,有且仅有一条直线与l平行,由平行公理得③正确;
④过直线l外一点P,有无数个平面与l平行,故④错误;
⑤与两个相交平面的交线平行的直线与两相交平面都平行或包含于一个平面中,故⑤错误;
⑥过空间内任意一点有且仅有一个平面与两条异面直线都平行,
当空间这一点在两条异面直线的一条上,不成立,故⑥错误;
⑦过空间内任意一点有且仅有一条直线与两条异面直线都相交,
当点在两条异面直线的一条直线上时,不成立,故⑦错误.
故答案为:②③.
点评:本题考查空间中两直线的位置关系的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
函数y=
定义域为( )
| x2+4 |
| A、{x|x≠0} |
| B、{x|x>2或x<-2} |
| C、R |
| D、{x|x≠±2} |
设S={x||x|<3},T={x|3x-5<1},则S∩T=( )
| A、∅ |
| B、{x|-3<x<3} |
| C、{x|-3<x<2} |
| D、{x|2<x<3} |
已知椭圆
+
=1上的一点M到焦点F1的距离为2,N是MF1的中点,O为原点,则|ON|等于( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、2 | ||
| B、4 | ||
| C、8 | ||
D、
|
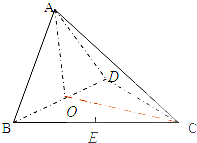 如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=