题目内容
椭圆
+
=1(a>b>0)的两个焦点是F1、F2,以|F1F2|为斜边作等腰直角三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:记椭圆的焦距为2C、依题意根据椭圆的对称性和勾股定理得:PF2=
c,最后利用e=
求得结果.
| ||
| 2 |
| 2c |
| 2a |
解答:
解:记椭圆的焦距为2C、依题意知点M在y轴上,交椭圆于P点,
不妨设F1、F2分别是双椭圆的左、右焦点,M在y轴正半轴上,则有F1(-c,0),M(0,c),
∴线段MP=
c.
利用勾股定理得:PF2=
c
又∵
=
=
即:e=
故选:C
不妨设F1、F2分别是双椭圆的左、右焦点,M在y轴正半轴上,则有F1(-c,0),M(0,c),
∴线段MP=
| ||
| 2 |
利用勾股定理得:PF2=
| ||
| 2 |
又∵
| 2c |
| 2a |
| 2c | ||||||||
|
| ||||
| 2 |
即:e=
| ||||
| 2 |
故选:C
点评:本题考查的知识点:窒息与双曲线的关系,双曲线的离心率,中点坐标公式及相关的运算问题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
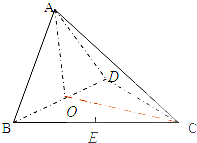 如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=
如图,在三棱锥A-BCD中,AO⊥平面BCD;O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=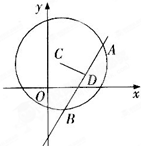 已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.