题目内容
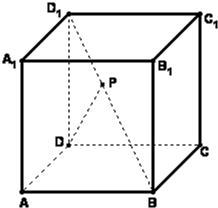如图，已知正方体ABCD-A1B1C1D1的棱长为a，点P在对角线BD1上，PD与面ABCD所成的角为45°．试建立空间直角坐标系，写出A，B，C，D，A1，B1，C1，D1，P，这9个点的坐标．考点：空间中的点的坐标
专题：计算题,空间位置关系与距离
分析：由已知中正方体ABCD-A1B1C1D1的棱长为a，P是正方形A1B1C1D1的中心点，易得到A、B、C、A1、B1、C1、D1、P的坐标；
解答：
解：如图建立空间直角坐标系，
则A（a，0，0），B（a，a，0），C（0，a，o），D（0，0，0），A1（a，0，a），B1（a，a，a），
C1（0，a，a），D1（0，0，a），P（(
-1)a，(
-1)a，(2-
)a）．
解：如图建立空间直角坐标系，则A（a，0，0），B（a，a，0），C（0，a，o），D（0，0，0），A1（a，0，a），B1（a，a，a），
C1（0，a，a），D1（0，0，a），P（(
| 2 |
| 2 |
| 2 |
点评：本题考查空间点的坐标表示，建立空间直角坐标系是解题的关键．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
相关题目
若a＞0＞b，0＞c＞d则以下不等式中不成立的是（ ）
| A、a+c＞b+d | ||||
| B、a-d＞b-c | ||||
| C、ac＜bd | ||||
D、
|
已知函数f（x）=2x+a•2-x（x∈R），则对于任意实数a，函数f（x）不可能是（ ）
| A、奇函数 | B、偶函数 |
| C、单调递增函数 | D、单调递减函数 |
下列四个函数中，既是偶函数又在（0，+∞）上为增函数的是（ ）
| A、f（x）=2x+1 | ||
| B、f（x）=2x2 | ||
C、f（x）=-
| ||
| D、f（x）=-|x| |