题目内容
数列{an}定义如下:a1=1,且当n≥2时,an=
,已知an=
,求正整数n.
|
| 30 |
| 19 |
考点:数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:先判断当n为偶数时,an>1;当n(n>1)是奇数时,an=
<1,由an=
>1,结合an=
,可得,a
=2-1=1,从而
=1,即可得出结论.
| 1 |
| an-1 |
| 30 |
| 19 |
|
| n-110 |
| 128 |
| n-110 |
| 128 |
解答:
解:由题设知,an>0,n=1,2,….
又由a1=1,可得,当n为偶数时,an>1;当n(n>1)是奇数时,an=
<1. …(4分)
由an=
>1,所以n为偶数,于是a
=
-1=
<1,
所以,
是奇数.
于是依次可得:a
-1=
>1,
-1是偶数,a
=
-1=
<1,
是奇数,
a
-1=
>1,
是偶数,a
=
-1=
<1,
是奇数,
a
-1=
>1,
是偶数,a
=
-1=
>1,
是偶数,
a
=
-1=
<1,
是奇数,…(9分)a
-1=
>1,
是偶数,a
=
-1=
<1,
是奇数,a
-1=2>1,
是偶数,a
=2-1=1,
所以,
=1,解得,n=238. …(14分)
又由a1=1,可得,当n为偶数时,an>1;当n(n>1)是奇数时,an=
| 1 |
| an-1 |
由an=
| 30 |
| 19 |
| n |
| 2 |
| 30 |
| 19 |
| 11 |
| 19 |
所以,
| n |
| 2 |
于是依次可得:a
| n |
| 2 |
| 19 |
| 11 |
| n |
| 2 |
| n-2 |
| 4 |
| 19 |
| 11 |
| 8 |
| 11 |
| n-2 |
| 4 |
a
| n-2 |
| 4 |
| 11 |
| 8 |
| n-6 |
| 4 |
| n-6 |
| 8 |
| 11 |
| 8 |
| 3 |
| 8 |
| n-6 |
| 8 |
a
| n-6 |
| 8 |
| 8 |
| 3 |
| n-14 |
| 8 |
| n-14 |
| 16 |
| 8 |
| 3 |
| 5 |
| 3 |
| n-14 |
| 16 |
a
| n-14 |
| 32 |
| 5 |
| 3 |
| 2 |
| 3 |
| n-14 |
| 32 |
| n-14 |
| 32 |
| 3 |
| 2 |
| n-46 |
| 32 |
| n-46 |
| 64 |
| 3 |
| 2 |
| 1 |
| 2 |
| n-46 |
| 64 |
| n-46 |
| 64 |
| n-110 |
| 64 |
| n-110 |
| 128 |
所以,
| n-110 |
| 128 |
点评:本题考查数列递推式,考查学生分析解决问题的能力,用倒推的方式是解题的关键.

练习册系列答案
相关题目
函数y=1-2sin2(x-
)是( )
| 3π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
(
-
)8 的展开式中的常数项为( )
| x |
| 1 | ||
|
| A、56 | B、70 | C、28 | D、60 |
某学校高中部组织赴美游学活动,其中高一240人,高二260人,高三300人,现需按年级抽样分配参加名额40人,高二参加人数为( )
| A、12 | B、13 | C、14 | D、15 |
 设计一个算法,输出区间[1,1000]内能被3和5整除的所有正整数,已知算法流程图如图,则图中空余部分可填写( )
设计一个算法,输出区间[1,1000]内能被3和5整除的所有正整数,已知算法流程图如图,则图中空余部分可填写( )| A、n>1000 |
| B、n≥1000 |
| C、n>999 |
| D、n≤999 |
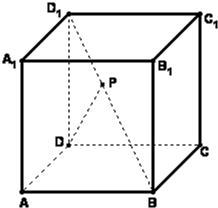 如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标. 如图,在平行四边形ABCD中,AB=x,BC=1,对角线AC与BD的夹角∠BOC=45°,记直线AB与CD的距离为h(x).求h(x)的表达式,并写出x的取值范围.
如图,在平行四边形ABCD中,AB=x,BC=1,对角线AC与BD的夹角∠BOC=45°,记直线AB与CD的距离为h(x).求h(x)的表达式,并写出x的取值范围.