题目内容
已知函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(2t)<0.
| ax+b |
| 1+x2 |
| 1 |
| 2 |
| 2 |
| 5 |
(1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(2t)<0.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)根据函数的奇偶性和条件,建立方程即可求函数f(x)的解析式;
(2)根据函数单调性的定义即可证明f(x)在(-1,1)上是增函数;
(3)根据函数的奇偶性将不等式f(t-1)+f(2t)<0进行转化,利用函数的单调性即可得到结论.
(2)根据函数单调性的定义即可证明f(x)在(-1,1)上是增函数;
(3)根据函数的奇偶性将不等式f(t-1)+f(2t)<0进行转化,利用函数的单调性即可得到结论.
解答:
解:(1)∵f(x)是(-1,1)上的奇函数,
∴f(0)=0,∴b=0.
又f(
)=
,
∴
=
,
∴a=1,
∴f(x)=
(2)证明:任设x1、x2∈(-1,1),且x1<x2
则f(x1)-f(x2)=
-
=
,
∵-1<x1<x2<1,
∴-1<x1x2<1,
∴x1-x2<0,且1-x1x2>0,
又1+
>0,1+
>0,
∴f(x1)-f(x2)<0
即f(t-1)<f(-t),
∴f(x)在(-1,1)上是增函数.
(3)∵f(x)是奇函数,
∴不等式可化为f(t-1)<-f(2t)=f(-2t)
即 f(t-1)<f(-2t),
又f(x)在(-1,1)上是增函数,
∴有
解之得0<t<
,
∴不等式的解集为{t|0<t<
}.
∴f(0)=0,∴b=0.
又f(
| 1 |
| 2 |
| 2 |
| 5 |
∴
| ||
1+(
|
| 2 |
| 5 |
∴a=1,
∴f(x)=
| x |
| 1+x2 |
(2)证明:任设x1、x2∈(-1,1),且x1<x2
则f(x1)-f(x2)=
| x1 | ||
1+
|
| x2 | ||
1+
|
| (x1-x2)(1-x1x2) | ||||
(1+
|
∵-1<x1<x2<1,
∴-1<x1x2<1,
∴x1-x2<0,且1-x1x2>0,
又1+
| x | 2 1 |
| x | 2 2 |
∴f(x1)-f(x2)<0
即f(t-1)<f(-t),
∴f(x)在(-1,1)上是增函数.
(3)∵f(x)是奇函数,
∴不等式可化为f(t-1)<-f(2t)=f(-2t)
即 f(t-1)<f(-2t),
又f(x)在(-1,1)上是增函数,
∴有
|
| 1 |
| 3 |
∴不等式的解集为{t|0<t<
| 1 |
| 3 |
点评:本题主要考查函数奇偶性的应用,以及函数单调性的证明和判断,综合考查函数性质的综合应用.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
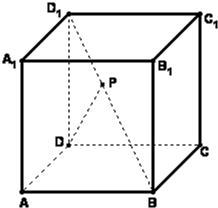 如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标. 如图,在平行四边形ABCD中,AB=x,BC=1,对角线AC与BD的夹角∠BOC=45°,记直线AB与CD的距离为h(x).求h(x)的表达式,并写出x的取值范围.
如图,在平行四边形ABCD中,AB=x,BC=1,对角线AC与BD的夹角∠BOC=45°,记直线AB与CD的距离为h(x).求h(x)的表达式,并写出x的取值范围.