题目内容
13.如图为某几何体的三视图,则其体积为( )
| A. | $\frac{14π}{6}+12$ | B. | $\frac{11π}{3}+4$ | C. | $\frac{11π}{6}+12$ | D. | $\frac{11π}{3}+12$ |
分析 由三视图还原原几何体,再由棱柱、球及圆锥的体积求解.
解答 解:由三视图还原原几何体如图,
下面是底面边长为2,高为3的正四棱柱,上面是半径为1的球,右边是底面半径为1,高为3的半圆锥.
其体积为V=$2×2×3+\frac{4}{3}π×{1}^{3}+\frac{1}{2}×\frac{1}{3}π×{1}^{2}×3$=$\frac{11π}{6}+12$.
故选:C.
点评 本题考查由三视图求组合体的体积,关键是由三视图还原原几何体,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.一位手机用户前四次输入四位数字手机密码均不正确,第五次输入密码正确,手机解锁.事后发现前四次输入的密码中,每次都有两个数字正确,但它们各自的位置均不正确.已知前四次输入密码分别为3406,1630,7364,6173,则正确的密码中一定含有数字( )
| A. | 4,6 | B. | 3,6 | C. | 3,7 | D. | 1,7 |
5.已知F1、F2分别为双曲线C:$\frac{x^2}{4}-\frac{y^2}{5}$=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
| A. | $\frac{4π}{15}$ | B. | $\frac{16π}{15}$ | C. | $\frac{64π}{15}$ | D. | $\frac{256π}{15}$ |
2.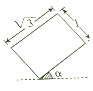 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
 一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )
一个放置在水平桌面上的正四棱柱的俯视图如图所示,其中α为锐角,则该几何体的正视图的面积的最大值为( )| A. | 2或3 | B. | 2$\sqrt{3}$或3 | C. | 1或3 | D. | 2或2$\sqrt{3}$ |