题目内容
已知函数y=
的值域是[-1，4]，求实数a，b的值．
| ax+b |
| x2-x+1 |
考点：函数的值域
专题：判别式法
分析：将分式化成整式，化为关于x的二次方程，由△≥0，得出关于y的不等式，-1和4是所对应的方程的两个根，代入即可求得a、b的值．
解答：
解：由y=
得yx2-（y+a）x+y-b=0，
①当y=0时，方程有解，适合题意思；
②当y≠0时，△=（y+a）2-4y（y-b）≥0，化简得，3y2-（2a+4b）y-a2≤0，
∵函数的值域为[-1，4]，∴-1，4是方程3y2-（2a+4b）y-a2=0的两根，
∴
解得
或
，
综上得：
或
．
| ax+b |
| x2-x+1 |
①当y=0时，方程有解，适合题意思；
②当y≠0时，△=（y+a）2-4y（y-b）≥0，化简得，3y2-（2a+4b）y-a2≤0，
∵函数的值域为[-1，4]，∴-1，4是方程3y2-（2a+4b）y-a2=0的两根，
∴
|
|
|
综上得：
|
|
点评：分母和分子次数最高为二次解析式，常用△法求函数的值域，即由△≥0得出关于y的不等式，求出y的取值范围．属于常规题．
练习册系列答案
相关题目
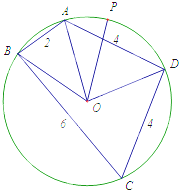已知圆内接四边形ABCD中，O为圆心，AB=2，BC=6，AD=CD=4．