题目内容
设函数f(x)=
(t≠0的常数).
(Ⅰ)若f(x)的单调递增区间是(0,e)(e是自然对数的底数),求t的取值范围;
(Ⅱ)若函数g(x)=(f(x))2+4f(x)+4只有一个零点,求t的取值范围;
(Ⅲ)若t>0,对任意x≥1,f(x)≤
恒成立,求t的取值范围.
| tlnx |
| x |
(Ⅰ)若f(x)的单调递增区间是(0,e)(e是自然对数的底数),求t的取值范围;
(Ⅱ)若函数g(x)=(f(x))2+4f(x)+4只有一个零点,求t的取值范围;
(Ⅲ)若t>0,对任意x≥1,f(x)≤
| (x2-1)t2 |
| x2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:根据导数与函数的单调性及最值的关系,通过解不等式求字母的取值范围,恒成立问题往往转化为求最值问题解决.
解答:
解:(1)∵f(x)=
(t≠0),∴f′(x)=t•
,
又题意可知f′(x)>0的解集是(0,e),而x∈(0,e)时,lnx<1即1-lnx>0,所以t>0.
综上所述,t的取值范围是(0,+∞)…4分
(2)由g(x)=[f(x)]2+4f(x)+4,得g(x)=[f(x)+2]2,
要使函数)=[f(x)]2+4f(x)+4只有一个零点,只需f(x)=-2有且只有一个实根,
∵f′(x)=t•
,令f′(x)=0得x=e,
x∈(0,e)时,1-lnx>0,x∈(e,+∞)时,1-lnx<0,
当t>0时,f(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
函数f(x)有最大值f(e)=
>0,但x(0,1)时,f(x)<0,x∈(1,+∞)时,f(x)>0,
此时f(x)=-2有且只有一个实根;
当t<0时,f(x)在(0,e)上单调递减,在(e,+∞)上单调递增,
函数f(x)有最大值f(e)=
<0,但x(0,1)时,f(x)>0,x∈(1,+∞)时,f(x)<0,
此时要使f(x)=-2有且只有一个实根,只需
=-2即t=-2e;
综上所述,t的取值范围是(0,+∞)∪{-2e}…9分
(3)由t>0时,对任意的x≥1都有f(x)≤
恒成立转化为
•t-lnx≥0恒成立.
令h(x)=
•t-lnx,则h′(x)=
•t-
=
,
由h′(x)=0得tx2-x+t=0,而△=1-4t2,
当t≥
时,△≤0,h′(x)≥0,所以h(x)在[1,+∞)上单调递增,h(x)≥h(1)=0符合题意;
当0<t<
时,tx2-x+t=0方程的两根x1=
<1,x2=
>1.
所以函数h(x)在[1,x2]上单调递减,h(x)≤h(1)=0,不符合题意;
综上所述,t的取值范围是[
,+∞]…14分
| tlnx |
| x |
| 1-lnx |
| x2 |
又题意可知f′(x)>0的解集是(0,e),而x∈(0,e)时,lnx<1即1-lnx>0,所以t>0.
综上所述,t的取值范围是(0,+∞)…4分
(2)由g(x)=[f(x)]2+4f(x)+4,得g(x)=[f(x)+2]2,
要使函数)=[f(x)]2+4f(x)+4只有一个零点,只需f(x)=-2有且只有一个实根,
∵f′(x)=t•
| 1-lnx |
| x2 |
x∈(0,e)时,1-lnx>0,x∈(e,+∞)时,1-lnx<0,
当t>0时,f(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
函数f(x)有最大值f(e)=
| t |
| e |
此时f(x)=-2有且只有一个实根;
当t<0时,f(x)在(0,e)上单调递减,在(e,+∞)上单调递增,
函数f(x)有最大值f(e)=
| t |
| e |
此时要使f(x)=-2有且只有一个实根,只需
| t |
| e |
综上所述,t的取值范围是(0,+∞)∪{-2e}…9分
(3)由t>0时,对任意的x≥1都有f(x)≤
| (x2-1)t2 |
| x2 |
| x2-1 |
| x |
令h(x)=
| x2-1 |
| x |
| x2+1 |
| x2 |
| 1 |
| x |
| t•x2-x+t |
| x2 |
由h′(x)=0得tx2-x+t=0,而△=1-4t2,
当t≥
| 1 |
| 2 |
当0<t<
| 1 |
| 2 |
1-
| ||
| 2t |
1+
| ||
| 2t |
所以函数h(x)在[1,x2]上单调递减,h(x)≤h(1)=0,不符合题意;
综上所述,t的取值范围是[
| 1 |
| 2 |
点评:本题考查利用导数研究函数的单调性以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件,注意等价转化.

练习册系列答案
相关题目
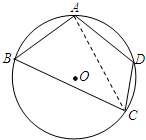 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,