题目内容
设数列{an}的首项不为零,前n项和为Sn,且对任意的r,t∈N*,都有
=(
)2.
(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3,bn=Sbn-1(n≥2,n∈N*),求证:数列{log3bn}为等比数列;
(3)在(2)的条件下,求Tn=
.
| Sr |
| St |
| r |
| t |
(1)求数列{an}的通项公式(用a1表示);
(2)设a1=1,b1=3,bn=Sbn-1(n≥2,n∈N*),求证:数列{log3bn}为等比数列;
(3)在(2)的条件下,求Tn=
| n |
 |
| k=2 |
| bk-1 |
| bk-1 |
考点:数列的求和,等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件推导出Sn=a1n2,由此能求出数列{an}的通项公式.
(2)由已知条件推导出bn=Sbn-1=bn-12,由此能证明数列{log3bn}是首项为1,公比为2的等比数列.
(3)由(2)推导出bn=32n-1(n∈N*).由此能求出Tn=
.
(2)由已知条件推导出bn=Sbn-1=bn-12,由此能证明数列{log3bn}是首项为1,公比为2的等比数列.
(3)由(2)推导出bn=32n-1(n∈N*).由此能求出Tn=
| n |
 |
| k=2 |
| bk-1 |
| bk-1 |
解答:
(1)解:因为a1=S1≠0,令t=1,r=n,
则
=(
)2,得
=n2,即Sn=a1n2.…2分
当n≥2时,an=Sn-Sn-1=a1(2n-1),
且当n=1时,此式也成立.
故数列{an}的通项公式为an=a1(2n-1).…5分
(2)证明:当a1=1时,由(1)知an=a1(2n-1)=2n-1,Sn=n2.
依题意,n≥2时,bn=Sbn-1=bn-12,…7分
于是log3bn=log3bn-12=2log3bn-1(n ≥ 2, n∈N),且log3b1=1,
故数列{log3bn}是首项为1,公比为2的等比数列.…10分
(3)解:由(2)得log3bn=1×2n-1=2n-1,
所以bn=32n-1(n∈N*).…12分
于是
=
=
=
-
.…15分
所以Tn=
=
(
-
)=
-
.…16分.
则
| Sr |
| St |
| r |
| t |
| Sn |
| S1 |
当n≥2时,an=Sn-Sn-1=a1(2n-1),
且当n=1时,此式也成立.
故数列{an}的通项公式为an=a1(2n-1).…5分
(2)证明:当a1=1时,由(1)知an=a1(2n-1)=2n-1,Sn=n2.
依题意,n≥2时,bn=Sbn-1=bn-12,…7分
于是log3bn=log3bn-12=2log3bn-1(n ≥ 2, n∈N),且log3b1=1,
故数列{log3bn}是首项为1,公比为2的等比数列.…10分
(3)解:由(2)得log3bn=1×2n-1=2n-1,
所以bn=32n-1(n∈N*).…12分
于是
| bk-1 |
| bk-1 |
| 32k-2 |
| 32k-1-1 |
| (32k-2+1)-1 |
| (32k-2+1)(32k-2-1) |
| 1 |
| 32k-2-1 |
| 1 |
| 32k-1-1 |
所以Tn=
| n |
 |
| k=2 |
| bk-1 |
| bk-1 |
| n |
 |
| k=2 |
| 1 |
| 32k-2-1 |
| 1 |
| 32k-1-1 |
| 1 |
| 2 |
| 1 |
| 32n-1-1 |
点评:本题考查数列的通项公式的求法,考查等比数列的证明,考查数列的前n项和求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
已知cosαcosβ=
,sin(
+α+β)=
,则sinαsinβ=( )
| 1 |
| 3 |
| π |
| 2 |
| 7 |
| 8 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
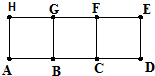 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.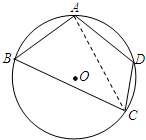 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,