题目内容
已知cosθ=-
,π<θ<
,求(sin
-cos
)2的值.
| 3 |
| 5 |
| 3π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由cosθ的值及θ的范围,利用同角三角函数间基本关系求出sinθ的值,原式利用完全平方公式化简,再利用同角三角函数间基本关系及二倍角的正弦函数公式化简,将sinθ的值代入计算即可求出值.
解答:
解:∵cosθ=-
,π<θ<
,
∴sinθ=-
=-
,
则(sin
-cos
)2=sin2
-2sin
cos
+cos2
=1-sinθ=1-(-
)=
.
| 3 |
| 5 |
| 3π |
| 2 |
∴sinθ=-
| 1-cos2θ |
| 4 |
| 5 |
则(sin
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| 4 |
| 5 |
| 9 |
| 5 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
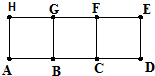 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.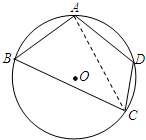 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米, 如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为
如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为