题目内容

已知ad≠bc，求证：（a2+b2）（c2+d2）＞（ac+bd）2．
考点：基本不等式
专题：证明题
分析：把（a2+b2）（c2+d2）-（ac+bd）2 展开化简化成完全平方的形式判断符号，可得其值大于或等于0，从而证得不等式成立．
解答： 解：因为（a2+b2）（c2+d2）-（ac+bd）2
=（a2c2+a2d2+b2c2+b2d2）-（a2c2+b2d2+2abcd）
=b2c2+a2d2-2abcd
=（bc-ad）2≥0
又ad≠bc
所以（bc-ad）2＞0
所以（a2+b2）（c2+d2）＞（ac+bd）2．
点评：本题考查用作差比较法证明不等式，式子的变形时解题的关键．
练习册系列答案
相关题目
以下程序运行结果为（　　）
t=1 
For i=2 To 5   
t=t*i   
Next    
输出t．
A、80B、95
C、100D、120
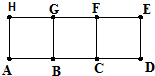已知长方形ADEH是由三个边长为1的正方形拼接而成的，从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ，当三点共线时ξ=0．
（1）求ξ=0时的概率；
（2）求ξ的分布列和Eξ．
已知函数f（x）=
x2+1
-ax，证明：当且仅当a≥1时，函数f（x）在区间[0，+∞）上是单调函数．
已知函数f（x）=
3
2
sin2x-cos2x-
1
2
（x∈R）
（1）当x∈[-
π
12
，
5π
12
]时，求函数f（x）取得最大值和最小值时x的值；
（2）设锐角△ABC的内角A、B、C的对应边分别是a，b，c，且a=1，c∈N*，若向量
m
=（1，sinA）与向量
n
=（2，sinB）平行，求c的值．
设各项都是正整数的无穷数列{an}满足：对任意n∈N*，有an＜an+1．记bn=aan．
（1）若数列{an}是首项a1=1，公比q=2的等比数列，求数列{bn}的通项公式；
（2）若bn=3n，证明：a1=2；
（3）若数列{an}的首项a1=1，cn=a an+1，{cn}是公差为1的等差数列．记dn=-2n•an，Sn=d1+d2+…+dn-1+dn，问：使Sn+n•2n+1＞50成立的最小正整数n是否存在？并说明理由．
已知函数y=
ax+b
x2-x+1
的值域是[-1，4]，求实数a，b的值．
已知在等比数列{an}中，2a2=a1+a3-1，a1=1．
（1）若数列{bn}满足b1+
b2
2
+
b3
3
+…+
bn
n
=an（n∈N*），求数列{bn}的通项公式；
（2）求数列{bn}的前n项和Sn．
如图矩形长为5，宽为2，在矩形内随机地撒200颗黄豆，数得落在阴影部分的黄豆数为120颗，则我们可以估计出阴影部分的面积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网