题目内容
求函数f（x）=x2-lnx2的单调区间．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：分别解出f′（x）＞0，令f′（x）＜0，即可得出．
解答：
解：f′(x)=2x-
=
（x≠0）．
令f′（x）＞0，解得x＞1或x＜-1；令f′（x）＜0，解得-1＜x＜0，或0＜x＜1．
∴函数f（x）的单调递增区间为（-∞，-1），（1，+∞）；
单调递减区间为（-1，0），（0，1）．
| 2 |
| x |
| 2x2-2 |
| x |
令f′（x）＞0，解得x＞1或x＜-1；令f′（x）＜0，解得-1＜x＜0，或0＜x＜1．
∴函数f（x）的单调递增区间为（-∞，-1），（1，+∞）；
单调递减区间为（-1，0），（0，1）．
点评：本题考查了利用导数研究函数的单调性，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
“α=kπ+
（k∈Z）”是“cos2α=
”的（ ）
| π |
| 6 |
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
函数f（x）=-2x2-x+1，x∈[-3，1]的最大值与最小值的和为（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
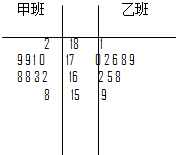最近我校对高一学生进行了体检，为了了解甲乙两班男生的身高状况，随机从甲乙两班中各抽取10名男生的身高（单位cm），绘制身高的茎叶图如图：
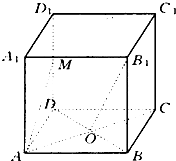在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，M为D1D的中点．