Question

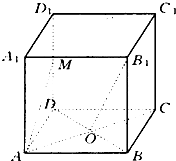在正方体ABCD-A₁B₁C₁D₁中，O为正方形ABCD的中心，M为D₁D的中点．
（Ⅰ）求证：异面直线B₁O与AM垂直；
（Ⅱ）求二面角B₁-AM-B的大小；
（Ⅲ）若正方体的棱长为a，求三棱锥B₁-AMC的体积．

Answer 1

考点：二面角的平面角及求法,棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）设AD的中点为N，连结ON，确定A₁N为B₁O在平面ADD₁A₁内的射影，证明Rt△A₁AN≌Rt△ADM，即可证明异面直线B₁O与AM垂直；
（Ⅱ）利用面积比，求二面角B₁-AM-B的大小；
（Ⅲ）由（Ⅰ）知，B₁O⊥平面AMC．所以V_B1-AMC=

1

3

B₁O×S_△AMC，即可求三棱锥B₁-AMC的体积．

解答： （Ⅰ）证明：设AD的中点为N，连结ON，
由O为正方形ABCD的中心，得ON⊥平面ADD₁A₁．
又AA₁⊥平面ADD₁A₁，所以A₁N为B₁O在平面ADD₁A₁内的射影．
在正方形ADD₁A₁中，Rt△A₁AN≌Rt△ADM，
∴∠AA₁N=∠MAD，
∴∠AA₁N+∠A₁AM=

π

2

，
∴A₁N⊥AM，
∴B₁O⊥AM；
（Ⅱ）解：设正方体的棱长为2，则AM=

5

，B₁A=2

2

，B₁M=3，∴cos∠MB₁A=

9+8-5

2×3×2 2

=

2

2

，
∴sin∠MB₁A=45°，
∴S△AB1M=

1

2

×3×2

2

×

2

2

=3，
△AMB中，AM=

5

，BA=2，BM=3，∴S_△AMB=

1

2

×2×

5

=

5

，
∴二面角B₁-AM-B的余弦值为

5

3

，
∴二面角B₁-AM-B的大小为arccos

5

3

；
（Ⅲ）解：由（Ⅰ）知，B₁O⊥平面AMC．所以V_B1-AMC=

1

3

B₁O×S_△AMC
因棱长为a，所以B₁O=

6

2

a，S_△AMC=

1

2

×MO×AC=

1

2

3

2

a

2

a=

6

4

a²
故V_B1-AMC=

1

3

×

6

2

a×

6

4

a²=

1

4

a³．

点评：本题考查二面角的平面角及求法，考查棱柱、棱锥、棱台的体积，考查学生分析解决问题的能力，属于中档题．