题目内容
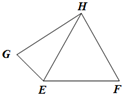 已知△EFH是边长为1的正三角形,动点G在平面EFH内.若
已知△EFH是边长为1的正三角形,动点G在平面EFH内.若| EG |
| EF |
| HG |
则
| HG |
| EF |
A、[-1,-
| ||||||
B、[-1,-
| ||||||
C、(-
| ||||||
D、(-
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,设出E,F,H,G的坐标,以及相应向量的坐标,运用向量的数量积的坐标表示和向量模的公式,结合圆的性质,可得x的范围为-1≤x≤1,再由条件即可得到计算得到.
解答:
 解:以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,
解:以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,
则E(-
,0),F(
,0),H(0,
),设G(x,y),
由|
|=1,可得x2+(y-
)2=1,
即有-1≤x≤1①
又
=(x+
,y),
=(1,0),
=(x,y-
).
由
•
<0,可得x+
<0,
即有x<-
②
由①②可得-1≤x<-
.
则
•
=x×1+(y-
)×0=x,
则所求范围为[-1,-
).
故选A.
 解:以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,
解:以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,则E(-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由|
| HG |
| ||
| 2 |
即有-1≤x≤1①
又
| EG |
| 1 |
| 2 |
| EF |
| HG |
| ||
| 2 |
由
| EG |
| EF |
| 1 |
| 2 |
即有x<-
| 1 |
| 2 |
由①②可得-1≤x<-
| 1 |
| 2 |
则
| HG |
| EF |
| ||
| 2 |
则所求范围为[-1,-
| 1 |
| 2 |
故选A.
点评:本题考查向量的数量积的坐标表示和向量模的公式,同时考查圆的性质和不等式的性质,属于中档题.

练习册系列答案
相关题目
已知a=2 -
,b=log2
,c=log23,则( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、a>b>c |
| B、z>c>b |
| C、c>b>a |
| D、c>a>b |
已知△ABC是边长为2的正三角形,则
•
的值为( )
| AB |
| BC |
| A、2 | ||
| B、-2 | ||
C、2
| ||
D、-2
|